一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.试求出该考生:
(Ⅰ)得60分的概率;(Ⅱ)得多少分的可能性最大?
(Ⅲ)所得分数ξ的数学期望(用小数表示,精确到0.k^s*5#u01).
(文科)投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个面中,有两个面的数字是0,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(Ⅰ)求点P落在区域C:x2+y2≤10上的概率;
(Ⅱ)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
分析:(Ⅰ)设“可判断两个选项是错误的”两道题之一选对的为事件A,“有一道题可判断一个选项是错误”选对的为事件B,“有一道题不理解题意”选对的为事件C,
P(A)=,
P(B)=,
P(C)=,由此能求出得60分的概率.
(Ⅱ)通过计算知得45分或50分的可能性最大.
(Ⅲ)
Eξ=40×+(45+50)×+55×+60×=≈47.92.
(文)(Ⅰ)点P的坐标有9种,其中落在区域C:x
2+y
2≤10上的点P的坐标有4种.由此能求出点P落在区域C:x
2+y
2≤10上的概率.
(Ⅱ)区域M为一边长为2的正方形,其面积为4,区域C的面积为10π,由此能求出豆子落在区域M上的概率.
解答:解:(Ⅰ)设“可判断两个选项是错误的”两道题之一选对的为事件A,“有一道题可判断一个选项是错误”选对的为事件B,“有一道题不理解题意”选对的为事件C,∴
P(A)=,
P(B)=,
P(C)=,∴得60分的概率为
P=×××=.(4分)
(Ⅱ)得45分或50分的可能性最大.
得40分的概率为:
P=×××=;
得45分的概率为:
P=××××+×××+×××=;
得50分的概率为:
P=×××+××××+××××+×××=;
得55分的概率为:
P=××××+×××+×××=.(8分)
(Ⅲ)
Eξ=40×+(45+50)×+55×+60×=≈47.92.(12分)
(文答案)解:(Ⅰ)点P的坐标有:
(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),(4,2),(4,4),共9种,其中落在区域C:x
2+y
2≤10上的点P的坐标有:(0,0),(0,2),(2,0),(2,2),共4种.故点P落在区域
C:x2+y2≤10上的概率为.(6分)
(Ⅱ)区域M为一边长为2的正方形,其面积为4,区域C的面积为10π,则豆子落在区域M上的概率为
.(12分)
点评:本题考查概率的性质和应用,解题时要认真审题,仔细解答,注意乘法公式的灵活运用.



 名校课堂系列答案
名校课堂系列答案![]() 的数学期望(用分数表示,精确到0.01).
的数学期望(用分数表示,精确到0.01).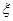 的数学期望(用小数表示,精确到0.01).
的数学期望(用小数表示,精确到0.01).