【题目】圆过点
，求
（1）周长最小的圆的方程；
（2）圆心在直线
上的圆的方程．
【答案】（1）
；（2）
.
【解析】试题分析:(1)当周长最小时
为圆的直径，由此可得所求圆的圆心和半径，即可得圆的方程；（2）线段
的垂直平分线与直线
的交点
即为圆心坐标, 
即为半径，可得圆的方程.
解:(1)当AB为直径时，过A、B的圆的半径最小，从而周长最小．即AB中点(0,1)为圆心，半径r＝
|AB|＝.则圆的方程为：x2＋(y－1)2＝10.
(2) 解法1：AB的斜率为k＝－3，则AB的垂直平分线的方程是y－1＝
x.即x－3y＋3＝0
由圆心在直线
上得两直线交点为圆心即圆心坐标是C(3,2)．
r＝|AC|＝
＝2.∴圆的方程是(x－3)2＋(y－2)2＝20.
解法2：待定系数法
设圆的方程为：(x－a)2＋(y－b)2＝r2.
则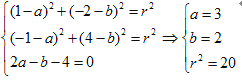
∴圆的方程为：(x－3)2＋(y－2)2＝20.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中，发现其在40分钟的一节课中，注意力指数
与听课时间
（单位：分钟）之间的关系满足如图所示的图象，当
时，图象是二次函数图象的一部分，其中顶点
，过点
；当
时，图象是线段
，其中
．根据专家研究，当注意力指数大于62时，学习效果最佳．
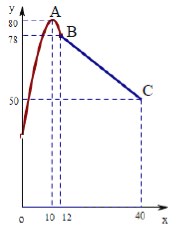
（1）试求
的函数关系式；
（2）教师在什么时段内安排内核心内容，能使得学生学习效果最佳？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
(
)是偶函数．
（1）求k的值；
（2）若函数
的图象与直线
没有交点，求
的取值范围；
（3）若函数
，
，是否存在实数
使得
最小值为
，若存在，求出
的值; 若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面直角坐标系
中，椭圆
的右焦点为
，离心率
，过点且垂直于
轴的直线被椭圆
截得的弦长为1.
（Ⅰ）求椭圆的方程；
（Ⅱ）记椭圆的上,下顶点分别为A,B，设过点
的直线
与椭圆分别交于点
，求证：直线
必定过一定点，并求该定点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了判断高中三年级学生选修文理科是否与性别有关，现随机抽取50名学生，得到2×2列联表：
理科 | 文科 | 总计 | |
男 | 13 | 10 | 23 |
女 | 7 | 20 | 27 |
总计 | 20 | 30 | 50 |
已知P(K2≥3.841)≈0.05，P(K2≥5.024)≈0.025.根据表中数据，得到K2≈4.844，则认为选修文理科与性别有关系出错的可能性约为________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下面是一段演绎推理：
大前提：如果直线平行于平面，则这条直线平行于平面内的所有直线；
小前提：已知直线b∥平面α，直线a平面α；
结论：所以直线b∥直线a.在这个推理中( )
A. 大前提正确，结论错误 B. 大前提错误，结论错误
C. 大、小前提正确，只有结论错误 D. 小前提与结论都是错误的
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个地区共有5个乡镇，共30万人，其人口比例为3∶2∶5∶2∶3，从这30万人中抽取一个300人的样本，分析某种疾病的发病率.已知这种疾病与不同的地理位置及水土有关，则应采取什么样的抽样方法?并写出具体过程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列表述正确的是（ ）
①归纳推理是由部分到整体的推理； ②归纳推理是由一般到一般的推理；
③演绎推理是由一般到特殊的推理； ④类比推理是由特殊到一般的推理；
⑤类比推理是由特殊到特殊的推理.
A. ①②③ B. ②③④ C. ②④⑤ D. ①③⑤
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列关于算法的说法，正确的序号是__________．
（1）一个问题的算法是唯一的；
（2）算法的操作步骤是有限的；
（3）算法的每一步操作必须是明确的，不能有歧义；
（4）算法执行后一定产生确定的结果．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com