定义y=log(1+x)F(x,y),x、y∈(0,+∞),
(Ⅰ)令函数f(x)=F(x,2)-3x,过坐标原点O作曲线C:y=f(x)的切线l,切点为P(n,t)(n>0),设曲线C与l及y轴围成图形的面积为S,求S的值.
(Ⅱ)令函数g(x)=F(x,2)+alnx,讨论函数g(x)是否有极值,如果有,说明是极大值还是极小值.
(Ⅲ)证明:当x,y∈N*且x<y时,F(x,y)>F(y,x).
【答案】
分析:(I)先确定切线方程,再利用定积分知识求面积;
(II)求导函数,确定函数的单调性,从而可求函数的极值;
(III)令

,证明h(x)在[1,+∞)上单调递减,1≤x<y时,
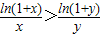
,从而可得结论.
解答:(I)解:∵y=log
(1+x)F(x,y),x、y∈(0,+∞),
∴f(x)=x
2-x+1,x∈(0,+∞),∴A(0,1),f′(x)=2x-1
∵过坐标原点O作曲线C:y=f(x)的切线l,切点为P(n,t)(n>0),
∴
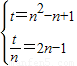
∴P(1,1),∴切线l的方程为y=x,
∴
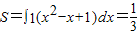
;
(II)解:∵g(x)=(1+x)
2+alnx,x∈(0,+∞)
∴
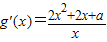
①△=4-8a≤0,即
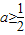
时,g′(x)≥0,
∴g(x)在(0,+∞)上单调递增,从而没有极值;
②当△=4-8a>0即
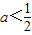
时,方程2x
2+2x+a=0有二个不等实根
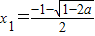
,
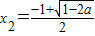
,
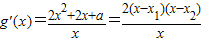
若
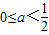
,则x
1<0,x
2≤0,g'(x)>0,
∴g(x)在(0,+∞)上单调递增,从而没有极值;
若a<0,则x
1<0,x
2>0,函数在(0,x
2)上,g'(x)<0,单调递减,在(x
2,+)上,g'(x)>0,单调递增
∴x=x
2,g(x)有极小值,没有极大值;
(III)证明:令
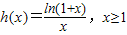
,则
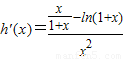
令p(x)=
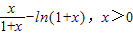
,则
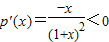
∴p(x)在(0,+∞)上单调递减
∴x>0时,p(x)<p(0)=0
∴x≥1时,h′(x)<0
∴h(x)在[1,+∞)上单调递减
∴1≤x<y时,
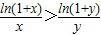
∴yln(1+x)>xln(1+y)
∴(1+x)
y>(1+y)
x∴F(x,y)>F(y,x).
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与极值,考查学生分析解决问题的能力,属于中档题.

 ,证明h(x)在[1,+∞)上单调递减,1≤x<y时,
,证明h(x)在[1,+∞)上单调递减,1≤x<y时,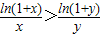 ,从而可得结论.
,从而可得结论.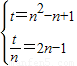
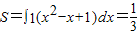 ;
;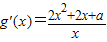
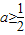 时,g′(x)≥0,
时,g′(x)≥0,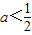 时,方程2x2+2x+a=0有二个不等实根
时,方程2x2+2x+a=0有二个不等实根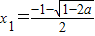 ,
,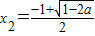 ,
,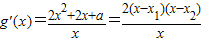
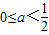 ,则x1<0,x2≤0,g'(x)>0,
,则x1<0,x2≤0,g'(x)>0,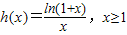 ,则
,则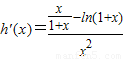
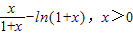 ,则
,则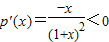
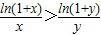


 阅读快车系列答案
阅读快车系列答案