练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    甲、乙、丙、丁四人并排站成一排，则甲或乙站在边上的概率为（　　）
    A、
    1
    6
    B、
    5
    6
    C、
    1
    2
    D、
    1
    3
    分析：先求出甲、乙、丙、丁四人并排站成一排的事件种数，然后求出甲和乙站在中间的情况，从而求出甲或乙站在边上的情况，最后利用古典概型的概率公式进行求解即可．
    解答：解：甲、乙、丙、丁四人并排站成一排一共有A44=24种
    甲和乙站在中间的情况有A22•A22=4种
    ∴甲或乙站在边上的情况有4种
    甲或乙站在边上的概率为
    20
    24
    =
    5
    6

    故选B．
    点评：本题求的是概率实际上本题考查的是排列问题，把排列问题包含在实际问题中，解题的关键是看清题目的实质，把实际问题转化为数学问题，解出结果以后再还原为实际问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：安徽省铜陵一中2011－2012学年高二6月月考数学理科试题 题型：044

    某县有甲乙丙丁四所高中的五千名学生参加了高三的调研测试，为了解数学学科的成绩情况，现从中随机抽取若干名学生在这次测试中的数学成绩作为样本，(其中甲学校抽取了30人)，制成如下频率分布表并得到相应的频率分布直方图：

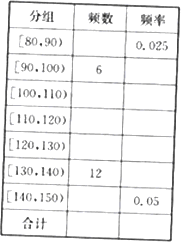
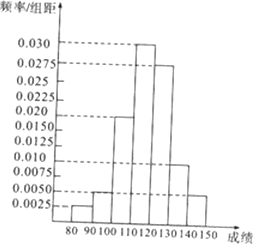
    (1)填写频率分布表．

    (2)该次统计中抽取样本的合理方法是什么，甲学校共有多少人参加了调研测试：

    (3)从样本在[80，100)的个体中任意抽取2个个体，求至少有一个个体落在[90，100)的概率．

    查看答案和解析>>

    科目：高中数学 来源：2010年本溪市高二下学期期末考试（理科）数学卷 题型：选择题

    甲、乙、丙、丁四位志愿者安排在周一至周日的7天中参加今年的上海世博志愿者活动，要求每人参加一天且每天至多安排一人,并要求甲排在乙的前面，则不同的方法有

      （A）280         （B）420         （C）840        （D）920

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校九年级学生共300人，为了解这个年级学生的体能，从中随机抽取部分学生进行1分钟的跳绳测试，并指定甲、乙、丙、丁四名同学对这次测试结果的数据作出整理，下面是这四名同学提供的部分信息：

    甲：将全体测试数据分成6组绘成直方图（如图）；

    乙：跳绳次数不少于105次的同学占96%；

    丙：第①、②两组频率之和为0.12，且第②组与第⑥组频数都是4；

    丁：第③组的频数比第④组的频数多2，且第③、④组的频数之和是第⑤组频数的4倍．

    根据这四名同学提供的材料，请解答如下问题：

    （1）这次跳绳测试共抽取多少名学生？第①、③组各有多少人？

    （2）如果跳绳次数不少于135次为优秀，根据这次抽查的结果，估计全年级达到跳绳优秀的人数为多少？

    （3）若分别以100、110、120、130、140、150作为第①、②、③、④、⑤、⑥组跳绳次数的代表，估计这批学生1分钟跳绳次数的平均值是多少？

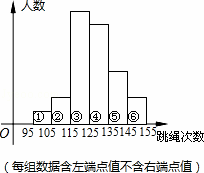
    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    甲、乙、丙、丁四位志愿者安排在周一至周日的7天中参加今年的上海世博志愿者活动，要求每人参加一天且每天至多安排一人，并要求甲排在乙的前面，则不同的方法有


    1. A.
      280
    2. B.
      420
    3. C.
      840
    4. D.
      920

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    甲、乙、丙、丁四人中选3人当代表,写出所有基本事件,并求甲被选上的概率_____

    查看答案和解析>>

    同步练习册答案