练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

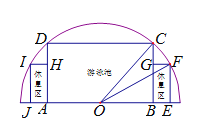
    【题目】如图，有一块半圆形空地，开发商计划建造一个矩形游泳池及左右两侧两个大小相同的矩形休息区，其中半圆的圆心为，半径为，矩形的一边在上，矩形的一边在上，点在圆周上，在直径上，且，设．若每平方米游泳池的造价与休息区造价之比为.

    （1）记游泳池及休息区的总造价为，求的表达式；

    （2）为进行投资预算，当为何值时，总造价最大？并求出总造价的最大值.

    【答案】（1）（2）当时，总造价最大值为.

    【解析】

    （1）根据几何关系，结合三角函数分别表示出面积，记可得到造价；

    （2）利用导函数结合三角函数性质讨论单调性求解最值.

    解：（1）设游泳池每平方米的造价为，休息区每平方米造价为，则在矩形中，，

    所以，.

    在矩形中，，

    所以，.

    所以，.

    （2）由（1）得，

    ，

    因为，所以.

    令，解得.因为，所以

    列表如下：

    0

    极大值

    所以，当时，总造价取得极大值，即最大值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】对某校高三年级100名学生的视力情况进行统计（如果两眼视力不同，取较低者统计），得到如图所示的频率分布直方图，已知从这100人中随机抽取1人，其视力在的概率为.

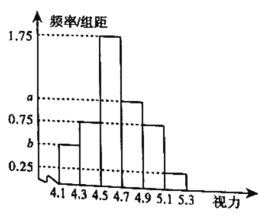
    （1）求a，b的值；

    （2）若报考高校A专业的资格为：任何一眼裸眼视力不低于5.0，已知在中有的学生裸眼视力不低于5.0.现用分层抽样的方法从和中抽取4名同学，设这4人中有资格（仅考虑视力）考A专业的人数为随机变量ξ，求ξ的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求在处的切线方程；

    （2）令，已知函数有两个极值点，且，

    ①求实数的取值范围；

    ②若存在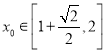，使不等式对任意（取值范围内的值）恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】网购已经成为一种新型的购物方式，2018年天猫双11，仅1小时47分钟成交额超过1000亿元，比2017年达到1000亿元的时间缩短了7个小时，为了研究市民对网购的依赖性，从A城市16﹣59岁人群中抽取一个容量为100的样本，得出下列2×2列联表，其中16﹣39岁为青年，40﹣59岁为中年，当日消费金额超过1000元为消费依赖网购，否则为消费不依赖网购．

    依赖网购

    不依赖网购

    小计

    青年（16﹣39岁）

    40

    20

    中年（40﹣59岁）

    20

    20

    小计

    （1）完成2×2列联表，计算X2值，并判断是否有95%的把握认为网购依赖和年龄有关？

    （2）把样本中的频率当作概率，随机从A城市中选取5人，其中依赖网购的人数为随机变量X，求随机变量X的分布列及期望（附：X2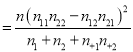，当X2＞3.841时，有95%的把握说事件A与B有关，当X2≤3.841时，没有95%的把握说事件A与B有关）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆：，，分别是椭圆短轴的上下两个端点，是椭圆的左焦点，P是椭圆上异于点，的点，若的边长为4的等边三角形．

    写出椭圆的标准方程；

    当直线的一个方向向量是时，求以为直径的圆的标准方程；

    设点R满足：，，求证：与的面积之比为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱，已知每个水箱的表面积为432（每个水箱的进出口所占面积与制作材料的厚度均忽略不计）．每个长方体水箱的底面长是宽的2倍．现设每个长方体水箱的底面宽是，用表示每个长方体水箱的容积．

    （1）试求函数的解析式及其定义域；

    （2）当为何值时，有最大值，并求出最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，.

    （1）当时，求的值域；

    （2）当时，不等式恒成立（是的导函数），求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.

    根据该走势图，下列结论正确的是（ ）

    A. 这半年中，网民对该关键词相关的信息关注度呈周期性变化

    B. 这半年中，网民对该关键词相关的信息关注度不断减弱

    C. 从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差

    D. 从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次高三年级统一考试中,数学试卷有一道满分10分的选做题,学生可以从,两道题目中任选一题作答.某校有900名高三学生参加了本次考试,为了了解该校学生解答该选做题的得分情况,计划从900名考生的选做题成绩中随机抽取一个容量为10的样本,为此将900名考生选做题的成绩按照随机顺序依次编号为001—900.

    （1）若采用随机数表法抽样,并按照以下随机数表,以加粗的数字5为起点,从左向右依次读取数据,每次读取三位随机数,一行读数用完之后接下一行左端.写出样本编号的中位数；

    05 26 93 70 60 22 35 85 15 13 92 03 51 59 77 59 56 78 06 83 52 91 05 70 74

    07 97 10 88 23 09 98 42 99 64 61 71 62 99 15 06 51 29 16 93 58 05 77 09 51

    51 26 87 85 85 54 87 66 47 54 73 32 08 11 12 44 95 92 63 16 29 56 24 29 48

    26 99 61 65 53 58 37 78 80 70 42 10 50 67 42 32 17 55 85 74 94 44 67 16 94

    14 65 52 68 75 87 59 36 22 41 26 78 63 06 55 13 08 27 01 50 15 29 39 39 43

    （2）若采用系统抽样法抽样,且样本中最小编号为08,求样本中所有编号之和：

    （3）若采用分层轴样,按照学生选择题目或题目,将成绩分为两层,且样本中题目的成绩有8个,平均数为7,方差为4：样本中题目的成绩有2个,平均数为8,方差为1.用样本估计900名考生选做题得分的平均数与方差.

    查看答案和解析>>

    同步练习册答案