
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() .
.
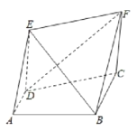
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 与
与![]() 轴交于
轴交于![]() 两点,且
两点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的一个动点,且直线
上的一个动点,且直线![]() 与直线
与直线![]() 分别交于
分别交于![]() 两点.是否存在点
两点.是否存在点![]() 使得以
使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,说明理由.
的横坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次![]() 公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:
公里的自行车个人赛中,25名参赛选手的成绩(单位:分钟)的茎叶图如图所示:

(1)现将参赛选手按成绩由好到差编为1~25号,再用系统抽样方法从中选取5人,已知选手甲的成绩为85分钟,若甲被选取,求被选取的其余4名选手的成绩的平均数;
(2)若从总体中选取一个样本,使得该样本的平均水平与总体相同,且样本的方差不大于7,则称选取的样本具有集中代表性,试从总体(25名参赛选手的成绩)选取一个具有集中代表性且样本容量为5的样本,并求该样本的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解高一学生的心理健康状况,某校心理健康咨询中心对该校高一学生的睡眠状况进行了抽样调查.该中心随机抽取了60名高一男生和40名高一女生,统计了他们入学第一个月的平均每天睡眠时间,得到如下频数分布表.规定:“平均每天睡眠时间大于等于8小时”为“睡眠充足”,“平均每天睡眠时间小于8小时”为“睡眠不足”.
高一男生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 3 | 20 | 19 | 10 | 8 |
高一女生平均每天睡眠时间频数分布表
睡眠时间(小时) |
|
|
|
|
|
频数 | 20 | 11 | 5 | 2 |
(1)请将下面的列联表补充完整,并根据已完成的![]() 列联表,判断是否有
列联表,判断是否有![]() 的把握认为“睡眠是否充足与性别有关”?
的把握认为“睡眠是否充足与性别有关”?
睡眠充足 | 睡眠不足 | 合计 | |
男生 | 42 | ||
女生 | 7 | ||
合计 | 100 |
(2)由样本估计总体的思想,根据这两个频数分布表估计该校全体高一学生入学第一个月的平均每天睡眠时间(同一组中的数据以这组数据所在区间中点的值作代表);
(3)若再从这100人中平均每天睡眠时间不足6小时的同学里随机抽取两人进行心理健康干预,则抽取的两人中包含女生的概率是多少?
附:参考公式:![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某书店销售刚刚上市的某高二数学单元测试卷,按事先拟定的价格进行5天试销,每种单价试销1天,得到如下数据:
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
(1)求试销![]() 天的销量的方差和
天的销量的方差和![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
附: 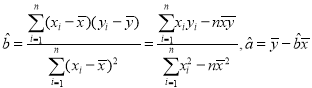 .
.
(2)预计以后的销售中,销量与单价服从上题中的回归直线方程,已知每册单元测试卷的成本是10元,为了获得最大利润,该单元测试卷的单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com