
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 f(x)是个周期为2的周期函数,且是个奇函数,在一个周期(-1,1)上,y=-sin$\frac{π}{2}$x,-1<f(x)<1,同理得到在其他周期上的图象;y=log4|x|是个偶函数,图象过(1,0),和(4,1),结合图象可得函数y=f(x)的图象与函数y=log4|x|的图象的交点个数,从而得到函数零点个数.
解答 解:由题意知,函数y=f(x)是个周期为2的周期函数,且是个奇函数,在一个周期(-1,1)上,y=-sin$\frac{π}{2}$x,-1<f(x)<1,同理得到在其他周期上的图象.
函数y=log4|x|是个偶函数,先看他们在[0,+∞)上的交点个数,则它们总的交点个数是在[0,+∞)上的交点个数的2倍,在(0,+∞)上,y=log4|x|=log4x,图象过(1,0),和(4,1),是单调增函数,与f(x)交与3个不同点,∴函数y=f(x)的图象与函数y=log4|x|的图象的交点个数是6个.
故选C.
点评 本题本题考查函数的周期性、奇偶性、函数图象的对称性,体现数形结合的数学思想.考查的知识点是根的存在性及根的个数判断,其中根据已知条件分析函数的性质,进而判断出函数零点的分布情况是解答本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
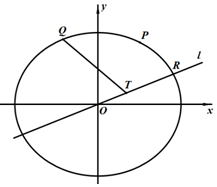 如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.
如图,在平面直角坐标系xOy中,点$P(1,\frac{3}{2})$和动点Q(m,n)都在离心率为$\frac{1}{2}$的椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)上,其中m<0,n>0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
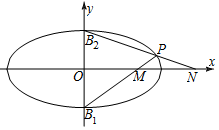 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴两端点为B1(0,-1)、B2(0,1),离心率e=$\frac{\sqrt{3}}{2}$,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴两端点为B1(0,-1)、B2(0,1),离心率e=$\frac{\sqrt{3}}{2}$,点P是椭圆C上不在坐标轴上的任意一点,直线B1P和B2P分别与x轴相交于M,N两点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4,6} | B. | {4,6} | C. | {3,4,6} | D. | {2,3,4,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com