
分析 (1)讨论a=0,a≠0时,运用奇偶性定义,即可判断;
(2)运用配方法,对a讨论,若a≤-$\frac{1}{2}$,a>-$\frac{1}{2}$,根据单调性,即可求得最小值.
解答 解:(1)当a=0时,函数f(-x)=(-x)2+|-x|+1=f(x),此时f(x)为偶函数.
当a≠0时,f(a)=a2+1,f(-a)=a2+2|a|+1,f(-a)≠f(a).
且f(-x)=x2+|-x-a|+1≠±f(x),
此时函数f(x)为非奇非偶函数.
(2)当x≥a时,函数$f(x)={x^2}+x-a+1={(x+\frac{1}{2})^2}-a+\frac{3}{4}$.
若a≤-$\frac{1}{2}$,则函数f(x)在[a,+∞)上的最小值为$f(-\frac{1}{2})=\frac{3}{4}-a$.
若a>-$\frac{1}{2}$,则函数f(x)在[a,+∞)上单调递增,
从而,函数f(x)在[a,+∞)上的最小值为f(a)=a2+1.
综上,当a≤-$\frac{1}{2}$时,函数f(x)的最小值是$\frac{3}{4}$-a.
当a>-$\frac{1}{2}$时,函数f(x)的最小值是a2+1.
点评 本题考查函数的奇偶性和最值的求法,注意运用分类讨论的思想方法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
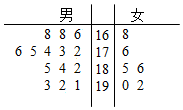 某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作.
某公司从大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分).公司规定:成绩在180分以上者到甲部门工作,180分以下者到乙部门工作,另外只有成绩高于180分的男生才能担任助理工作. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
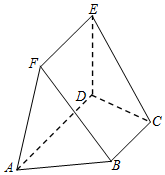 如图,在五面体ACDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°,AB=4,DE=EF=2.
如图,在五面体ACDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°,AB=4,DE=EF=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9\sqrt{2}}{2}$ | B. | $\frac{9\sqrt{2}}{4}$ | C. | $\frac{9\sqrt{2}}{8}$ | D. | 9$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
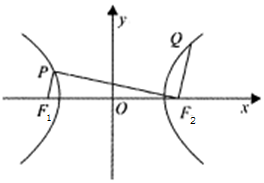 设F1,F2为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,P,Q分别为双曲线左、右支上的点,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,则双曲线的离心率为( )
设F1,F2为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,P,Q分别为双曲线左、右支上的点,若$\overrightarrow{Q{F_2}}$=2$\overrightarrow{P{F_1}}$,且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$═0,则双曲线的离心率为( )| A. | $\frac{{\sqrt{15}}}{3}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{7}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3x+1 | B. | f(x)=$\frac{1}{x}$ | C. | f(x)=1-$\frac{1}{x}$ | D. | f(x)=x3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com