
【题目】在平面直角坐标系中,点![]() ,
,![]() 分别为椭圆C:
分别为椭圆C:![]() 的左右焦点,椭圆
的左右焦点,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上,不在
在椭圆C上,不在![]() 轴上的动点P与动点Q关于原点O对称,且四边形
轴上的动点P与动点Q关于原点O对称,且四边形![]() 的周长为
的周长为![]() .
.
(1)求动点P的轨迹方程;
(2)在动点P的轨迹上有两个不同的点M![]() ,N
,N![]() ,线段MN的中点为G,已知点
,线段MN的中点为G,已知点![]() 在圆
在圆![]() 上,求
上,求![]() 的最大值,并判断此时ΔOMN的形状.
的最大值,并判断此时ΔOMN的形状.
【答案】(1)![]() ;(2)最大值为
;(2)最大值为![]() ,ΔOMN是直角三角形
,ΔOMN是直角三角形
【解析】
(1)题中先求得![]() 的坐标,即
的坐标,即![]() ,可利用离心率
,可利用离心率![]() 和点
和点![]() 在椭圆上
在椭圆上 ![]() 结合
结合![]() 解得
解得![]()
![]() ,动点P与动点Q关于原点O对称,且四边形
,动点P与动点Q关于原点O对称,且四边形![]() 的周长为
的周长为![]() .可得
.可得![]() 点轨迹是椭圆,且长轴长已知,焦距已知,只要再求得短半轴长
点轨迹是椭圆,且长轴长已知,焦距已知,只要再求得短半轴长![]() 即得,注意方程中
即得,注意方程中![]() ;
;
(2)由![]() 用点
用点![]() 都在椭圆上可求得
都在椭圆上可求得![]() ,用两点间距离公式表示出
,用两点间距离公式表示出![]() ,代入
,代入![]() 和
和![]() ,并利用基本不等式可求得最大值.根据取得最大值时的条件得
,并利用基本不等式可求得最大值.根据取得最大值时的条件得![]() 是直角三角形.
是直角三角形.
(1)设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]()
![]()
由已知可知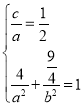 ,又
,又![]() ,所以可得
,所以可得![]() ,则
,则![]() ,
,![]()
连接PQ,因为![]() ,OP=OQ,所以四边形
,OP=OQ,所以四边形![]() 为平行四边形.
为平行四边形.
因为四边形![]() 的周长为
的周长为![]() ,所以
,所以![]() ,
,
所以动点P的轨迹是以点![]() ,
,![]() 分别为左、右焦点,长轴长为
分别为左、右焦点,长轴长为![]() 的椭圆(除去左、右顶点),可得动点P的轨迹方程为
的椭圆(除去左、右顶点),可得动点P的轨迹方程为![]()
(2)因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,
,
所以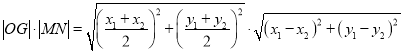
![]() .
.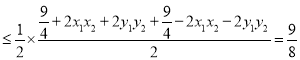
当且仅当![]() ,即
,即![]() 时,等号成立,
时,等号成立,
所以![]() 的最大值为
的最大值为![]() ,此时
,此时![]() ,即
,即![]() ,即
,即![]() 是直角三角形.
是直角三角形.


科目:高中数学 来源: 题型:
【题目】2019年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备,通过市场分析,全年需投入固定成本3000万元,每生产x(百辆),需另投入成本![]() 万元,且
万元,且 ,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
,由市场调研知,每辆车售价6万元,且全年内生产的车辆当年能全部销售完.
(1)求出2019年的利润![]() (万元)关于年产量x(百辆)的函数关系式;(利润=销售额
(万元)关于年产量x(百辆)的函数关系式;(利润=销售额![]() 成本)
成本)
(2)2019年产量为多少(百辆)时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四边形![]() 中,
中,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,如图(1),将其沿
,如图(1),将其沿![]() 折起使得平面
折起使得平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,连接
,连接![]() ,如图(2).
,如图(2).
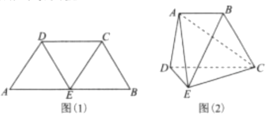
(1)证明:图(2)中的![]() 四点共面;
四点共面;
(2)求图(2)中平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第28届金鸡百花电影节将于11月19日至23日在福建省厦门市举办,近日首批影展片单揭晓,《南方车站的聚会》《春江水暖》《第一次的离别》《春潮》《抵达之谜》五部优秀作品将在电影节进行展映.若从这五部作品中随机选择两部放在展映的前两位,则《春潮》与《抵达之谜》至少有一部被选中的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江心洲有一块如图所示的江边,![]() ,
,![]() 为岸边,岸边形成
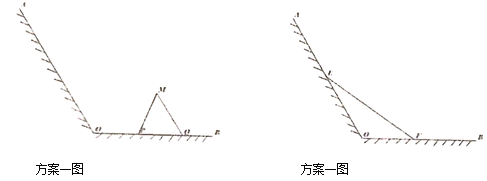
为岸边,岸边形成![]() 角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边
角,现拟在此江边用围网建一个江水养殖场,有两个方案:方案l:在岸边![]() 上取两点
上取两点![]() ,用长度为
,用长度为![]() 的围网依托岸边线
的围网依托岸边线![]() 围成三角形
围成三角形![]() (
(![]() ,
,![]() 两边为围网);方案2:在岸边
两边为围网);方案2:在岸边![]() ,
,![]() 上分别取点
上分别取点![]() ,用长度为
,用长度为![]() 的围网
的围网![]() 依托岸边围成三角形
依托岸边围成三角形![]() .请分别计算
.请分别计算![]() ,
,![]() 面积的最大值,并比较哪个方案好.
面积的最大值,并比较哪个方案好.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求实数m的值;
(2)若α≥1,β≥1,f(α)+f(β)=4,求证:![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,点E在BC上,
,点E在BC上,![]() .
.
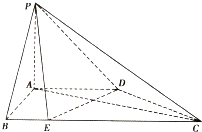
(1)求证:平面![]() 平面PAC;
平面PAC;
(2)若直线PE与平面PAC所成的角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年2月13日《烟台市全民阅读促进条例》全文发布,旨在保障全民阅读权利,培养全民阅读习惯,提高全民阅读能力,推动文明城市和文化强市建设.某高校为了解条例发布以来全校学生的阅读情况,随机调查了200名学生每周阅读时间![]() (单位:小时)并绘制如图所示的频率分布直方图.
(单位:小时)并绘制如图所示的频率分布直方图.

(1)求这200名学生每周阅读时间的样本平均数![]() 和中位数
和中位数![]() (
(![]() 的值精确到0.01);
的值精确到0.01);
(2)为查找影响学生阅读时间的因素,学校团委决定从每周阅读时间为![]() ,
,![]() 的学生中抽取9名参加座谈会.
的学生中抽取9名参加座谈会.
(i)你认为9个名额应该怎么分配?并说明理由;
(ii)座谈中发现9名学生中理工类专业的较多.请根据200名学生的调研数据,填写下面的列联表,并判断是否有![]() 的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
的把握认为学生阅读时间不足(每周阅读时间不足8.5小时)与“是否理工类专业”有关?
阅读时间不足8.5小时 | 阅读时间超过8.5小时 | |
理工类专业 | 40 | 60 |
非理工类专业 |
附:![]() (
(![]() ).
).
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| <> | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com