
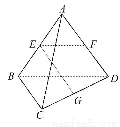
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算:
(1)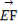 ·
·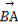 .
.
(2)EG的长.
(3)异面直线EG与AC所成角的大小.
(1) 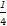 (2)
(2)  (3) 45°
(3) 45°
【解析】设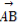 =a,
=a,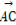 =b,
=b, =c,
=c,
则|a|=|b|=|c|=1,
<a,b>=<b,c>=<c,a>=60°, =
=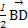 =
=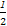 c-
c-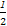 a,
a,
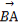 =-a,
=-a,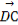 =b-c.
=b-c.
(1) ·
·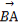 =(
=(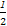 c-
c-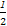 a)·(-a)
a)·(-a)
=-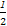 a·c+
a·c+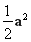 =-
=-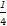 +
+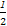 =
=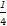 .
.
(2)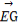 =
=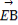 +
+ +
+
= +(
+(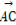 -
-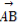 )+
)+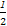 (
( -
-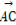 )
)
=- +
+ +
+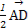 =-
=-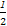 a+
a+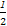 b+
b+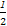 c
c
∴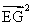 =
=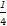 (-a+b+c)2
(-a+b+c)2
=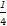 (
( -2a·b-2a·c+2b·c)=
-2a·b-2a·c+2b·c)=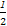 ,
,
∴|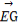 |=
|= ,即EG的长为
,即EG的长为 .
.
(3)由(2)知,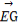 ·
·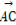 =(-
=(-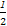 a+
a+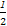 b+
b+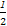 c)·b
c)·b
=-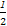 a·b+
a·b+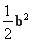 +
+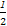 c·b=
c·b=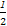 ,
,
∴cos<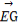 ,
,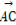 >=
>=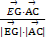 =
=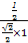 =
= .
.
故异面直线EG与AC所成的角为45°.
【方法技巧】用向量法解题的常见类型及常用方法
1.常见类型
利用向量可解决空间中的平行、垂直、长度、夹角等问题.
2.常用的解题方法
(1)基向量法
先选择一组基向量,把其他向量都用基向量表示,然后根据向量的运算解题.
(2)坐标法
根据条件建立适当的空间直角坐标系,并求出相关点的坐标,根据向量的坐标运算解题即可.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十八第七章第七节练习卷(解析版) 题型:填空题
在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE与BD的位置关系是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:解答题
如图,已知正四棱锥P-ABCD的所有棱长都是2,底面正方形两条对角线相交于O点,M是侧棱PC的中点.
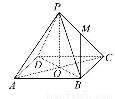
(1)求此正四棱锥的体积.
(2)求直线BM与侧面PAB所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十三第七章第二节练习卷(解析版) 题型:选择题
某几何体的三视图如图所示,则该几何体的体积为( )
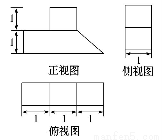
(A) (B)2 (C)
(B)2 (C) (D)3
(D)3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:填空题
在空间直角坐标系中,以点A(4,1,9),B(10,-1,6),C(x,4,3)为顶点的△ABC是以BC为斜边的等腰直角三角形,则实数x的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:选择题
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若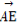 =
=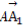 +x
+x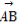 +y
+y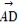 ,则x,y的值分别为( )
,则x,y的值分别为( )
(A)x=1,y=1 (B)x=1,y=
(C)x= ,y=
,y= (D)x=
(D)x= ,y=1
,y=1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十一第六章第七节练习卷(解析版) 题型:选择题
用数学归纳法证明不等式1+ +
+ +…+
+…+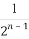 >
>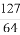 (n∈N*)成立,其初始值至少应取( )
(n∈N*)成立,其初始值至少应取( )
(A)7 (B)8 (C)9 (D)10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十四第二章第十一节练习卷(解析版) 题型:选择题
函数y=(3-x2)ex的单调递增区间是( )
(A)(-∞,0)
(B)(0,+∞)
(C)(-∞,-3)和(1,+∞)
(D)(-3,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com