
【题目】设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(参考数据: ![]() .
.
(2)证明: ![]() ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 ![]() .令
.令 ![]() 的值.
的值.
【答案】
(1)
解:由题意得f'(x)=(r+1)(1+x)r﹣(r+1)=(r+1)[(1+x)r﹣1],
令f'(x)=0,解得x=0.
当﹣1<x<0时,f'(x)<0,∴f(x)在(﹣1,0)内是减函数;
当x>0时,f'(x)>0,∴f(x)在(0,+∞)内是增函数.
故函数f(x)在x=0处,取得最小值为f(0)=0.
(2)
证明:由(1),当x∈(﹣1,+∞)时,有f(x)≥f(0)=0,
即(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>﹣1且x≠0,有(1+x)r+1>1+(r+1)x,①
在①中,令 ![]() (这时x>﹣1且x≠0),得
(这时x>﹣1且x≠0),得 ![]() .
.
上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),
即 ![]() ,②
,②
当n>1时,在①中令 ![]() (这时x>﹣1且x≠0),
(这时x>﹣1且x≠0),
类似可得 ![]() ,③
,③
且当n=1时,③也成立.
综合②,③得 ![]() ,④
,④
(3)
解:在④中,令 ![]() ,n分别取值81,82,83,…,125,
,n分别取值81,82,83,…,125,
得 ![]() ,
, ![]() ,
, ![]() ,…
,… ![]() ,
,
将以上各式相加,并整理得 ![]() .
.
代入数据计算,可得 ![]()
由[S]的定义,得[S]=211.
【解析】(1)先求出函数f(x)的导函数f′(x),令f'(x)=0,解得x=0,再求出函数的单调区间,进而求出最小值为f(0)=0;(2)根据(1)知,即(1+x)r+1≥1+(r+1)x,令 ![]() 代入并化简得
代入并化简得 ![]() ,再令
,再令 ![]() 得,
得, ![]() ,即结论得到证明;(3)根据(Ⅱ)的结论,令
,即结论得到证明;(3)根据(Ⅱ)的结论,令 ![]() ,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得,
,n分别取值81,82,83,…,125,分别列出不等式,再将各式相加得, ![]() ,再由参考数据和条件进行求解.
,再由参考数据和条件进行求解.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性和数列的前n项和的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;数列{an}的前n项和sn与通项an的关系
在这个区间单调递减;数列{an}的前n项和sn与通项an的关系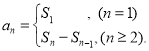 .
.


科目:高中数学 来源: 题型:
【题目】某企业用180万元购买一套新设备,该套设备预计平均每年能给企业带来100万元的收入,为了维护设备的正常运行,第一年需要各种维护费用10万元,且从第二年开始,每年比上一年所需的维护费用要增加10万元
(1)求该设备给企业带来的总利润![]() (万元)与使用年数
(万元)与使用年数![]() 的函数关系;
的函数关系;
(2)试计算这套设备使用多少年,可使年平均利润最大?年平均利润最大为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得 ![]() ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定区域D:  .令点集T={(x0 , y0)∈D|x0 , y0∈Z,(x0 , y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定条不同的直线.
.令点集T={(x0 , y0)∈D|x0 , y0∈Z,(x0 , y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定条不同的直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还”,其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,则该人第五天走的路程为( )
A. 6里B. 12里C. 24里D. 48里
查看答案和解析>>
科目:高中数学 来源: 题型:
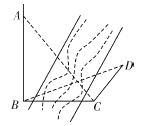
【题目】如图,为测得河对岸塔![]() 的高,先在河岸上选一点
的高,先在河岸上选一点![]() ,使
,使![]() 在塔底
在塔底![]() 的正东方向上,测得点
的正东方向上,测得点![]() 的仰角为60°,再由点
的仰角为60°,再由点![]() 沿北偏东15°方向走
沿北偏东15°方向走![]() 到位置
到位置![]() ,测得
,测得![]() ,则塔
,则塔![]() 的高是(单位:
的高是(单位:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示,则下列说法正确的是( )
的图象如图所示,则下列说法正确的是( )

A. 函数![]() 的周期为
的周期为![]()
B. 函数![]() 在
在![]() 上单调递增
上单调递增
C. 函数![]() 的图象关于点
的图象关于点![]() 对称
对称
D. 把函数![]() 的图象向右平移
的图象向右平移![]() 个单位,所得图象对应的函数为奇函数
个单位,所得图象对应的函数为奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com