
分析 由f(x)在点x=0连续,$\underset{lim}{x→0}$$\frac{sin6x+{e}^{-3ax}-1}{3x}$=f(a),根据等价无穷小代换,即可求得a的值.
解答 解:f(x)=$\left\{\begin{array}{l}{\frac{sin6x+{e}^{-3ax}-1}{3x},x≠0}\\{a,x=0}\end{array}\right.$在点x=0连续,
由等价无穷小代换:sin6x=6x,e-3ax-1=-3ax,
∴$\underset{lim}{x→0}$$\frac{sin6x+{e}^{-3ax}-1}{3x}$=$\underset{lim}{x→0}$$\frac{6x-3ax}{3x}$=2-a,
∴2-a=a,
∴a=1,
故答案为:1.
点评 本题考查函数在某点连续,等价无穷小代换,考查分析问题及解决问题得能力,属于中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
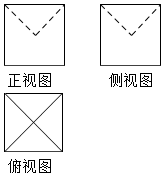 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,两条虚线互相垂直且相等,则该几何体的体积是( )| A. | $\frac{20}{3}$ | B. | $\frac{16}{3}$ | C. | $8-\frac{π}{6}$ | D. | $8-\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
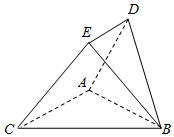 如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.
如图,以BC为斜边的等腰直角三角形ABC与等边三角形ABD所在平面互相垂直,且点E满足$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{AC}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
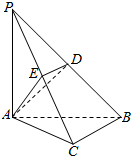 如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.
如图,在三棱锥P-ABC中,PA⊥底面ABC,点D,E分别在棱PB、PC上,PA=AB=2,∠ABC=60°,∠BCA=90°,且DE∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{6})$ | B. | $(1,\sqrt{6})$ | C. | $(\sqrt{3},\sqrt{6})$ | D. | $(\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com