
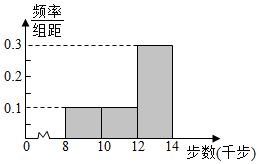
 王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.
王师傅为响应国家开展全民健身运动的号召,每天坚持“健步走”,并用计步器对每天的“健步走”步数进行统计,他从某个月中随机抽取10天“健步走”的步数,绘制出的频率分布直方图如图所示.| 每天的步数分组 (千步) | [8,10) | [10,12) | [12,14] |
| 评价级别 | 及格 | 良好 | 优秀 |
分析 (1)由频率分布直方图,能估计该月王师傅每天“健步走”的步数的中位数及平均数.
(2)设评价级别是“良好”或“及格”的这4天分别为a1,a2,b1,b2,由此利用列举法能求出从统计的这10天中评价级别是“良好”或“及格”的天数里随机抽取的2天,属于同一评价级别的概率.
解答 解:(1)由频率分布直方图,
得中位数为:12+$\frac{1}{6}×2$=$\frac{37}{3}$≈12.3(千步),
平均数为:0.2×9+0.2×11+0.6×13=11.8(千步).
(2)设评价级别是“良好”或“及格”的这4天分别为a1,a2,b1,b2,
则从这4天中任意抽取2天,总的抽法有:a1a2,a1b1,a1b2,a2b1,a2b2,b1b2,共6种.
所抽取的2天属于同一评价级别的情况只有a1a2,b1b2,共2种.
∴从统计的这10天中评价级别是“良好”或“及格”的天数里随机抽取的2天,
属于同一评价级别的概率是$\frac{1}{3}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
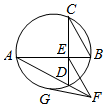 如图,E是圆内两弦AB和CD的交点,F为AD延长线上一点,FG切圆于G,且FE=FG.
如图,E是圆内两弦AB和CD的交点,F为AD延长线上一点,FG切圆于G,且FE=FG.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知an=2n-1,n∈N*,将数列{an}的项依次按如图的规律“蛇形排列”成一个金字塔状的三角形数阵,其中第m行有2m-1个项,记第m行从左到右的第k个数为bm,k(1≤k≤2m-1,m,k∈N*),如b3,4=15,b4,2=29,则bm,k=$\left\{\begin{array}{l}{2{m}^{2}-4m+k+1,m为奇数}\\{2{m}^{2}-2k+1,m为偶数}\end{array}\right.$(结果用m,k表示).
已知an=2n-1,n∈N*,将数列{an}的项依次按如图的规律“蛇形排列”成一个金字塔状的三角形数阵,其中第m行有2m-1个项,记第m行从左到右的第k个数为bm,k(1≤k≤2m-1,m,k∈N*),如b3,4=15,b4,2=29,则bm,k=$\left\{\begin{array}{l}{2{m}^{2}-4m+k+1,m为奇数}\\{2{m}^{2}-2k+1,m为偶数}\end{array}\right.$(结果用m,k表示).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com