
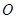 为圆心,
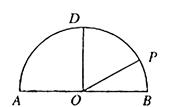
为圆心,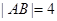 为直径的半圆
为直径的半圆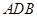 中,
中,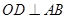 ,
,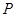 是半圆弧上一点,
是半圆弧上一点,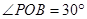 ,曲线
,曲线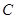 是满足
是满足 为定值的动点
为定值的动点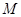 的轨迹,且曲线
的轨迹,且曲线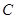 过点
过点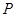 .
.
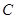 的方程;
的方程;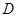 的直线l与曲线
的直线l与曲线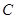 相交于不同的两点
相交于不同的两点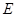 、
、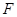
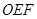 的面积不小于
的面积不小于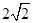 ,求直线
,求直线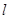 斜率的取值范围.
斜率的取值范围. 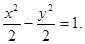 (Ⅱ) [-
(Ⅱ) [-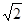 ,-1]∪(-1, 1)∪(1,
,-1]∪(-1, 1)∪(1,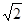 ).
). 为定值,可确定点M的轨迹是双曲线,
为定值,可确定点M的轨迹是双曲线,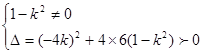
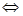
 ,从而得到k的取值范围.
,从而得到k的取值范围.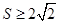 ,得到关于k的不等式,从而解出k的取值范围,再与前面k的取值范围求交集即可.
,得到关于k的不等式,从而解出k的取值范围,再与前面k的取值范围求交集即可.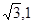 ),依题意得
),依题意得 <|AB|=4.
<|AB|=4.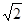 ,∴a2=2,b2=c2-a2=2.∴曲线C的方程为
,∴a2=2,b2=c2-a2=2.∴曲线C的方程为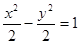 .
.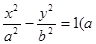 >0,b>0).
>0,b>0).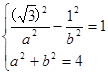 解得a2=b2=2,∴曲线C的方程为
解得a2=b2=2,∴曲线C的方程为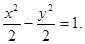
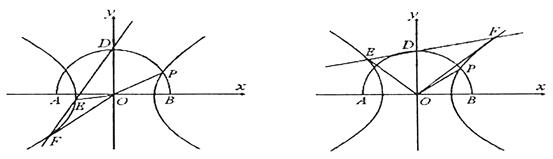
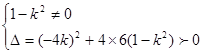
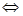

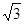 ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,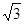 ).
).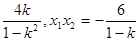 ,于是
,于是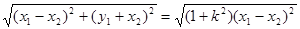
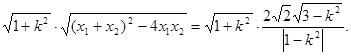
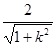 ,
,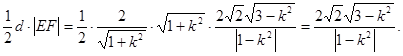
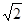 ,即S△OEF
,即S△OEF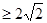 ,则有
,则有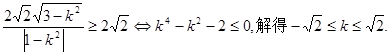 ③
③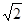 ,-1]∪(1-,1) ∪(1,
,-1]∪(1-,1) ∪(1, 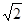 ).
).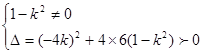
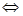

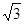 ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,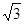 ).
).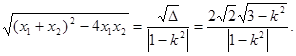 ③
③
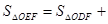 S△ODE=
S△ODE=
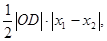 于是
于是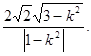

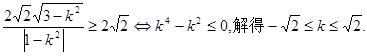 ④
④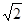 ,-1]∪(-1, 1)∪(1,
,-1]∪(-1, 1)∪(1,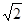 ).
).

科目:高中数学 来源:不详 题型:解答题
 ,
, 是平面上一动点,且满足
是平面上一动点,且满足 ,
, 的轨迹
的轨迹 对应的方程;
对应的方程; 在曲线
在曲线 上,过点
上,过点 作曲线
作曲线 的两条弦
的两条弦 ,且
,且 的斜率为
的斜率为 满足
满足 ,试判断动直线
,试判断动直线 是否过定点,并证明你的结论.
是否过定点,并证明你的结论.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
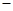 3,0),C(3,0)另两边所在直线的斜率之积为
3,0),C(3,0)另两边所在直线的斜率之积为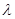 (
(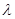 为常数),则顶点A的轨迹不可能落在下列哪一种曲线上( )
为常数),则顶点A的轨迹不可能落在下列哪一种曲线上( )| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com