
【题目】某种水果按照肉质和口感可分为四类:标准果,优质果,精品果,礼品果,某采购商从采购的一批水果中随机抽取100个(每个水果的重量相当),利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)用样本估计总体,果园老板提出两种购销方案给采购商参考:
方案①:不分类卖出,单价为20元/![]() .
.
方案②:分类卖出,分类后的水果售价如下表:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/ | 16 | 18 | 22 | 24 |
从采购商的角度考虑,应该采用哪种方案较好?并说明理由.
(2)从这100个水果中用分层抽样的方法抽取10个,再从抽取的10个水果中随机抽取2个,求抽取的2个水果不是同一级别水果的概率.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|-![]() x(a>0).
x(a>0).
(1)若a=3,解关于x的不等式f(x)<0;
(2)若对于任意的实数x,不等式f(x)-f(x+a)<a2+![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]()
(3)在(2)条件下,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率是
的离心率是![]() ,一个顶点是
,一个顶点是![]() .
.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
,![]() 是椭圆
是椭圆![]() 上异于点
上异于点![]() 的任意两点,且
的任意两点,且![]() .试问:直线
.试问:直线![]() 是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
是否恒过一定点?若是,求出该定点的坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中,边长为2,E为AB中点,F是边BC上的动点.
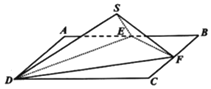
(1)将△ADE沿DE翻折90°到△SDE,求二面角S-DC-E的正切值;
(2)若![]() ,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求
,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求下列各式中x,y的值:
(1)若![]() ,则
,则![]() ______________;
______________;
(2)若![]() ,则
,则![]() ___________;
___________;
(3)若![]() ,则
,则![]() ____________;
____________;
(4)若![]() ,则
,则![]() _____________;
_____________;
(5)若![]() ,则
,则![]() ________________;
________________;
(6)若![]() ,则
,则![]() _____________,
_____________,![]() __________;
__________;
(7)若![]() ,则
,则![]() _______________.
_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,其中一个焦点与抛物线
的中心在原点,其中一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的左右焦点分别为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,求以
,求以![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆的方程.
相切的圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com