练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．设log29=a，log35=b，用a，b的代数表示lg2=$\frac{2}{2+ab}$．

    分析 log29=a，log35=b，可得$\frac{lg3}{lg2}$=$\frac{a}{2}$，$\frac{lg5}{lg3}$=b．化简代入即可得出．

    解答 解：∵log29=a，log35=b，∴$\frac{lg3}{lg2}$=$\frac{a}{2}$，$\frac{lg5}{lg3}$=b．
    ∴1-lg2=lg5=b×$\frac{a}{2}$lg2，
    解得lg2=$\frac{2}{2+ab}$．
    故答案为：$\frac{2}{2+ab}$．

    点评 本题考查了对数的运算性质、换底公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．对任意的实数R，集合A={x|x2+x-6＞0}，B={-1，0，1，2，3，4}．则B∩∁RA=（　　）
    A．{2，3，4，5}B．{-1，0}C．{-1，0，1，2}D．{ 2，3，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．给出下面几个函数：（1）y=x-3，（2）y=x2，（3）$y={x^{\frac{4}{3}}}$，（4）y=3x，（5）y=log0.3x其中是奇函数的个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点M到左焦点F1的距离是2，N是MF1的中点，O为坐标原点，则|ON|的值为（　　）
    A．4B．8C．3D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

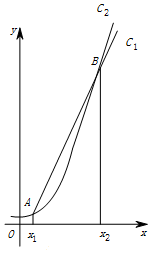    14．函数f（x）=2x和g（x）=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．若x1∈[a，a+1]，x2∈[b，b+1]，且a，b∈{1，2，3，4，5，6，7，8，9，10，11，12}，则a+b=10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知函数f（x）=x2-mx+1的两个零点分别在区间（0，1）和（1，2），则实数m的取值范围（2，$\frac{5}{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

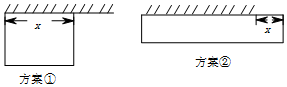    11．上海市复兴高级中学二期改扩建工程于2015年9月正式开始，现需要围建一个面积火900平方米的矩形地场地的围墙，有一面长度为20米的旧墙（图中斜杠部），有甲、乙两种维修利用旧墙方案．
    甲方案：选取部分旧墙（选取的旧墙的长度设为x米，x∈（0，20]），维修后单独作为矩形场地的一面围墙（如方案①图），多余部分不维修；
    乙方案：旧墙全部利用维修后，再续建一段新墙（新墙的长度高x米），共同作为矩形场地的一面（如方案②图）
    已知旧墙维修费用为10元/米，新墙造价为80元/米，设修建总费用y．
    （1）如果按甲方案修建，试用解析式将修建总费用y1表示成关于x的函数；
    （2）如果按乙方案修建，试用解析式将修建总费用y2表示成关于x的函数；
    （3）试求出两种方案中修建总费用y1，y2的最小值，并比较哪种方案最节省费用？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．不等式3x2-7x-10≥0的解集是{x|x≥$\frac{10}{3}$或x≤-1}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．△ABC的三边AB、BC、CA所在的直线方程分别是5x-y-12=0，x+3y+4=0，x-5y+12=0．求：
    （1）经过点C且到原点的距离为7的直线方程；
    （2）BC边上的高所在的直线方程．

    查看答案和解析>>

    同步练习册答案