
【题目】已知曲线C1的参数方程为 ![]() (其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(其中θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0.
(1)分别写出曲线C1与曲线C2的普通方程;
(2)若曲线C1与曲线C2交于A,B两点,求线段AB的长.
【答案】
(1)解:曲线C1的参数方程为 ![]() (其中θ为参数),消去参数θ可得:曲线
(其中θ为参数),消去参数θ可得:曲线 ![]() .
.
曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0,可得直角坐标方程:曲线C2:x﹣y+1=0
(2)解:联立 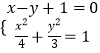 ,得7x2+8x﹣8=0,
,得7x2+8x﹣8=0,
设A(x1,y1),B(x2,y2),则 ![]() ,
, ![]() ,
,
于是 ![]() .
.
故线段AB的长为 ![]()
【解析】(1)曲线C1的参数方程为 ![]() (其中θ为参数),利用平方关系消去参数θ可得曲线C1的普通方程.曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0,利用互化公式可得直角坐标方程.(2)直线方程与椭圆联立可得7x2+8x﹣8=0,利用一元二次方程的根与系数的关系、弦长公式即可得出.
(其中θ为参数),利用平方关系消去参数θ可得曲线C1的普通方程.曲线C2的极坐标方程为ρcosθ﹣ρsinθ+1=0,利用互化公式可得直角坐标方程.(2)直线方程与椭圆联立可得7x2+8x﹣8=0,利用一元二次方程的根与系数的关系、弦长公式即可得出.


科目:高中数学 来源: 题型:
【题目】从边长为2a的正方形铁片的四个角各截去一个边长为x的正方形,然后折成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正数t.
(1)把铁盒的容积V表示为关于x的函数,并指出其定义域.
(2)当x为何值时,容积V有最大值?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x-mx+n,m,n∈R.
(1)若函数f(x)的图像在点(1,f(1))处的切线为y=2x-1,求m,n的值;
(2)求函数f(x)的单调区间;
(3)若n=0,不等式f(x)+m<0对x∈(1,+∞)恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用![]() 表示.
表示.
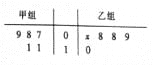
(1)若乙组同学投篮命中次数的平均数比甲组同学的平均数少1,求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(2)在(1)的条件下,分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名,求这两名同学的投篮命中次数之和为16的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形.点E是棱PC的中点,平面ABE与棱PD交于点F.
(Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=AD,且平面PAD⊥平面ABCD,求证:AF⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com