
【题目】等腰直角△![]() 内接于抛物线
内接于抛物线![]() (
(![]() ),其中
),其中![]() 为抛物线的顶点,
为抛物线的顶点,![]() ,△
,△![]() 的面积是16.
的面积是16.
(1)求抛物线![]() 的方程;
的方程;
(2)抛物线![]() 的焦点为
的焦点为![]() ,过
,过![]() 的直线交抛物线于
的直线交抛物线于![]()
![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,若
,若![]() ,
,![]() ,证明:
,证明:![]() 是一个定值.
是一个定值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人轮流吹同一只气球,当且仅当气球内的气体体积![]() (单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或
(单位:毫升)大于2014时,气球会被吹破.先由甲开始吹入1毫升气体,约定以后每次吹入的气体体积为上一次体积的2倍或![]() ,且吹入的气体体积为整数.
,且吹入的气体体积为整数.
(1)若谁先吹破气球谁输,问谁有必胜策略?证明你的结论.
(2)若在不吹破气球的前提下,约定单次吹入的气体体积最大者为赢家(如果吹入的体积相同,则最先吹出最大体积者为赢家).问:谁有必胜策略?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】擎天柱为了防止魔方落入霸天虎手中,打算用激光刀将其销毁.擎天柱使用的方法是:每次切割可将魔方分成两个体积之比为![]() 的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有
的六面体,每个六面体恰包含魔方的一个面,且任两次操作得到的截面在魔方中均有交点,而魔方的属性决定每次切割只能暂时将它割开,而无法分离,且只要它有![]() 的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
的小正方体区域始终未被割到,就无法被销毁,证明:无论擎天柱切割多少次,均无法销毁魔方.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的农机具零配件,为了预测今年7月份该型号农机具零配件的市场需求量,以合理安排生产,工厂对本年度1月份至6月份该型号农机具零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的6组数据如下表所示:
(单位:千件)之间的6组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价 | 11.1 | 9.1 | 9.4 | 10.2 | 8.8 | 11.4 |
销售量 | 2.5 | 3.1 | 3 | 2.8 | 3.2 | 2.4 |
(1)根据1至6月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)结合(1)中的线性回归方程,假设该型号农机具零配件的生产成本为每件3元,那么工厂如何制定7月份的销售单价,才能使该月利润达到最大?(计算结果精确到0.1)
参考公式:回归直线方程![]() ,
,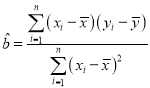
参考数据:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,下列对函数
,下列对函数![]() 的性质描述正确的是( )
的性质描述正确的是( )
A.函数![]() 的图象关于点
的图象关于点![]() 对称
对称
B.若![]() ,则函数f(x)有极值点
,则函数f(x)有极值点
C.若![]() ,函数
,函数![]() 在区间
在区间![]() 单调递减
单调递减
D.若函数![]() 有且只有3个零点,则a的取值范围是
有且只有3个零点,则a的取值范围是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新冠状肺炎疫情牵动每一个中国人的心,危难时刻众志成城,共克时艰,为疫区助力.福建省漳州市东山县共101个海鲜商家及个人为缓解武汉物质压力,募捐价值百万的海鲜输送武汉.东山岛,别称陵岛,形似蝴蝶亦称蝶岛,隶属于福建省漳州市东山县,是福建省第二大岛,中国第七大岛,介于厦门市和广东省汕头之间,东南是著名的闽南渔场和粤东渔场交汇处,因地理位置发展海产品养殖业具有得天独厚的优势.根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布![]() .
.
(1)随机购买10只该商家的海产品,求至少买到一只质量小于265克该海产品的概率;
(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入![]() (千元)与年收益增量
(千元)与年收益增量![]() (千元).
(千元).![]() 的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线
的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
.根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
附:若随机变量![]() ,则
,则![]()
![]() ;
;
对于一组数据![]()
![]()
![]()
![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为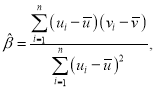
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com