
【题目】某同学计划用他姓名的首字母![]() ,身份证的后4位数字(4位数字都不同)以及3个符号
,身份证的后4位数字(4位数字都不同)以及3个符号![]() 设置一个六位的密码.若
设置一个六位的密码.若![]() 必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
必选,且符号不能超过两个,数字不能放在首位和末位,字母和数字的相对顺序不变,则他可设置的密码的种数为( )
A.864B.1009C.1225D.1441
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,焦距为
,焦距为![]() ,直线
,直线![]() 过椭圆的
过椭圆的![]() 左焦点.
左焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() 是椭圆
是椭圆![]() 上的两个动点,
上的两个动点,![]() 的平分线在
的平分线在![]() 轴上,
轴上,![]() .试判断直线
.试判断直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某地区小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
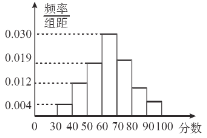
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)若将频率视为概率,从该地区小学的这些学生中随机抽取3人,记这3人中成绩位于区间![]() 内的人数为
内的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足n≥2时,
满足n≥2时,![]() ,则称数列
,则称数列![]() (n
(n![]() )为
)为![]() 的“L数列”.
的“L数列”.
(1)若![]() ,且
,且![]() 的“L数列”为
的“L数列”为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() 的“L数列”为递增数列,求k的取值范围;
的“L数列”为递增数列,求k的取值范围;
(3)若![]() ,其中p>1,记
,其中p>1,记![]() 的“L数列”的前n项和为
的“L数列”的前n项和为![]() ,试判断是否存在等差数列
,试判断是否存在等差数列![]() ,对任意n
,对任意n![]() ,都有
,都有![]() 成立,并证明你的结论.
成立,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六,八是中国人的吉利数字,所以好多器都做成六棱形和八棱形,数学李老师有一个正六棱柱形状的笔筒,底面边长为6cm,高为18cm(底部及筒壁厚度忽略不计),一长度为![]() cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
cm的圆铁棒l(粗细忽略不计)斜放在笔筒内部,l的一端置于正六柱某一侧棱的展端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为_____cm2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面ABCD.
平面ABCD.
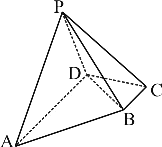
(1)求证:![]() ;
;
(2)在线段PA上是否存在一点M,使二面角M-BC-D的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
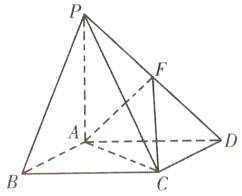
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com