【题目】如图，在三棱锥
中，
，
在底面
上的射影为
，
于点
.
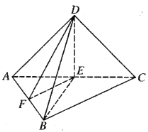
（1）求证：平面
平面
；
（2）若
，求直线
与平面
所成的角的余弦值.
【答案】（1）证明见解析；（2）
.
【解析】
（1）先证明
平面
，又
平面
，从而证明平面
平面；（2）由
平面
，
易知
，则
为
的中点，过点作
于点
，可证
平面
，则
即为
与平面所成的角，最后根据条件和
求出
即可得到结果.
（1）证明：由题意知平面，平面，
所以
，又
，
，所以平面，
又平面，所以平面平面；
（2）由平面，易知
.
则，所以为的中点，
过点作于点，如图：
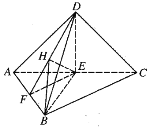
则由（1）知平面平面，又平面
平面
，
则平面，所以即为与平面所成的角，
由
，
得
，
，
又
，且E为AC中点，则
，
中，
，
根据可得，
，
所以
，则
，
所以与平面所成的角的余弦值为.
【点晴】
本题考查面面垂直的证明和线面所成角的求解，几何法求线面所成角关键在于确定高的位置和长度，属中档题.
寒假乐园北京教育出版社系列答案科目：高中数学 来源： 题型：
【题目】在单位圆O：x2+y2＝1上任取一点P（x，y），圆O与x轴正向的交点是A，设将OA绕原点O旋转到OP所成的角为θ，记x，y关于θ的表达式分别为x＝f（θ），y＝g（θ），则下列说法正确的是（ ）
A.x＝f（θ）是偶函数，y＝g（θ）是奇函数
B.x＝f（θ）在
为增函数，y＝g（θ）在为减函数
C.f（θ）+g（θ）≥1对于
恒成立
D.函数t＝2f（θ）+g（2θ）的最大值为
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】请从下面三个条件中任选一个，补充在下面的横线上，并作答．
①AB⊥BC，②FC与平面ABCD所成的角为
，③∠ABC
．
如图，在四棱锥P﹣ABCD中，底面ABCD是菱形，PA⊥平面ABCD，且PA＝AB＝2，，PD的中点为F．
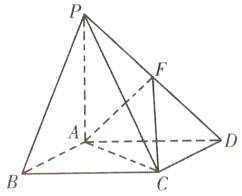
（1）在线段AB上是否存在一点G，使得AF
平面PCG？若存在，指出G在AB上的位置并给以证明；若不存在，请说明理由；
（2）若_______，求二面角F﹣AC﹣D的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某科研团队对
例新冠肺炎确诊患者的临床特征进行了回顾性分析.其中
名吸烟患者中，重症人数为
人，重症比例约为
；
名非吸烟患者中，重症人数为
人，重症比例为
.根据以上数据绘制
列联表，如下：
吸烟人数 | 非吸烟人数 | 总计 | |
重症人数 | 30 | 120 | 150 |
轻症人数 | 100 | 800 | 900 |
总计 | 130 | 920 | 1050 |
(1)根据列联表数据，能否在犯错误的概率不超过
的前提下认为新冠肺炎重症和吸烟有关？
(2)已知每例重症患者平均治疗费用约为
万元，每例轻症患者平均治疗费用约为
万元.现有吸烟确诊患者20人，记这
名患者的治疗费用总和为
，求
.
附：
|
|
|
|
|
|
|
|
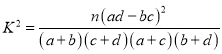
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知如图一
，
，
，
，
分别为
，
的中点，
在
上，且
，
为
中点，将
沿
折起，
沿
折起，使得
，
重合于一点（如图二），设为
．
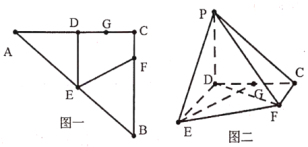
（1）求证：
平面
；
（2）求二面角
的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
