
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数![]() 模型.园区服务中心P在x轴正半轴上,PO=
模型.园区服务中心P在x轴正半轴上,PO=![]() 百米.
百米.

(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道直线段PQ最短.
【答案】(1) ![]() 的最小值为
的最小值为![]() 百米.
百米.
(2) 当点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米,通道PQ最短.
百米,通道PQ最短.
【解析】
(1)设![]() ,
,![]() ,求出
,求出![]()
![]() ,再利用基本不等式求OM的最短长度.(2) 当直线
,再利用基本不等式求OM的最短长度.(2) 当直线![]() 与边界曲线相切时,
与边界曲线相切时,![]() 最短.设切点为
最短.设切点为![]() ,求出切点为
,求出切点为![]() ,切线方程为
,切线方程为![]() ,令
,令![]() ,得
,得![]() ,即点
,即点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米.
百米.
(1)设![]() ,
,![]() ,
,
则![]()
![]()
![]() ,
,
当且仅当![]() ,即
,即![]() 时取等号.
时取等号.
所以![]() 的最小值为
的最小值为![]() 百米.
百米.
(2)当直线![]() 与边界曲线相切时,
与边界曲线相切时,![]() 最短.
最短.
设切点为![]() ,由
,由![]() 得
得![]() ,
,
所以切线的方程为![]() .
.
因为![]() 在
在![]() 轴正半轴上,且PO=
轴正半轴上,且PO=![]() ,所以
,所以![]() 点坐标为
点坐标为![]() .
.
因为切线过点![]() ,所以
,所以![]() ,
,
整理得![]() ,解得
,解得![]() ,或
,或![]() .
.
因为![]() ,所以
,所以![]() ,此时切点为
,此时切点为![]() ,切线方程为
,切线方程为![]() .
.
令![]() ,得
,得![]() ,即点
,即点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米.
百米.
答:当点![]() 在线段
在线段![]() 上且距离
上且距离![]() 轴
轴![]() 百米,通道PQ最短.
百米,通道PQ最短.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]()
![]() 为参数
为参数![]() 以原点为极点x轴正半轴为极轴建立极坐标系,直线
以原点为极点x轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着小汽车的普及,“驾驶证”已经成为现代人“必考”证件之一.若某人报名参加了驾驶证考试,要顺利地拿到驾驶证,需要通过四个科目的考试,其中科目二为场地考试在每一次报名中,每个学员有![]() 次参加科目二考试的机会(这
次参加科目二考试的机会(这![]() 次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试,或
次考试机会中任何一次通过考试,就算顺利通过,即进入下一科目考试,或![]() 次都没有通过,则需要重新报名),其中前
次都没有通过,则需要重新报名),其中前![]() 次参加科目二考试免费,若前
次参加科目二考试免费,若前![]() 次都没有通过,则以后每次参加科目二考试都需要交
次都没有通过,则以后每次参加科目二考试都需要交![]() 元的补考费.某驾校通过几年的资料统计,得到如下结论:男性学员参加科目二考试,每次通过的概率均为
元的补考费.某驾校通过几年的资料统计,得到如下结论:男性学员参加科目二考试,每次通过的概率均为![]() ,女性学员参加科目二考试,每次通过的概率均为
,女性学员参加科目二考试,每次通过的概率均为![]() .现有一对夫妻同时报名参加驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
.现有一对夫妻同时报名参加驾驶证考试,在本次报名中,若这对夫妻参加科目二考试的原则为:通过科目二考试或者用完所有机会为止.
(1)求这对夫妻在本次报名中参加科目二考试都不需要交补考费的概率;
(2)求这对夫妻在本次报名中参加科目二考试产生的补考费用之和为![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知抛物线![]() 和圆
和圆![]() 的公共弦过抛物线的焦点
的公共弦过抛物线的焦点![]() ,且弦长为4.
,且弦长为4.
(1)求抛物线和圆的方程;
(2)过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 两点抛物线在点
两点抛物线在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
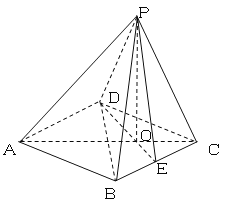
【题目】如图,已知四棱锥P-ABCD的底面是边长为2的菱形,∠BCD=60°,点E是BC边
的中点,AC,DE交于点O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求证:PD⊥BC;
(2)在线段AP上找一点F,使得BF∥平面PDE,并求此时四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
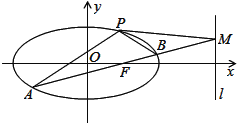
【题目】如图,已知椭圆C:![]() 的离心率为
的离心率为![]() ,并且椭圆经过点P(1,
,并且椭圆经过点P(1,![]() ),直线l的方程为x=4.
),直线l的方程为x=4.
(1)求椭圆的方程;
(2)已知椭圆内一点E(1,0),过点E作一条斜率为k的直线与椭圆交于A,B两点,交直线l于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数![]() ,使得k1+k2=
,使得k1+k2=![]() k3?若存在,求出
k3?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 数列
数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() (
(![]() 为常数).
为常数).
(1)当![]() 时,求
时,求![]() ;
;
(2)当![]() 时,
时,
(ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(ⅱ)若对任意![]() ,必存在
,必存在![]() 使得
使得![]() ,已知
,已知![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若![]() 是
是![]() 的中点,直线
的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段BP的长度.
,求线段BP的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
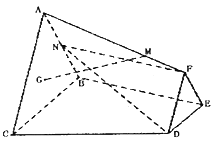
【题目】如图,已知![]() 与
与![]() 分别是边长为1与2的正三角形,
分别是边长为1与2的正三角形,![]() ,四边形
,四边形![]() 为直角梯形,且
为直角梯形,且![]() ,
,![]() ,点
,点![]() 为
为![]() 的重心,
的重心,![]() 为
为![]() 中点,
中点,![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点.
的三等分点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的余弦值为
的余弦值为![]() ,试求异面直线
,试求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com