
对一批共50件的某电器进行分类检测,其重量(克)统计如下:

规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有"A"型2件
(1)从该批电器中任选1件,求其为“B"型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率
(1) 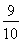 ; (2)
; (2)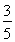
【解析】
试题分析:(1) 依题意规定重量在85克及以上的为“B”型,又因为小于85的共有5件,所以大于或等于85的共有50-5=45件.即B型的共有45件.所以从该批电器中任选1件,求其为“B"型的概率即可求得.
(2)由于从5件电器中任取两件总共有10种情况,而其中有两件是A型电器,所以其中恰有1件为“A”型情况通过列举共有6种情况.即可求出结论.
试题解析:(1)设“从该批电器中任选1件,其为”B”型”为事件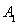 ,
,
则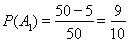 所以从该批电器中任选1件,求其为”B”型的概率为
所以从该批电器中任选1件,求其为”B”型的概率为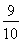 .
.
(2)设“从重量在[80,85)的5件电器中,任选2件电器,求其中恰有1件为”A”型”为事件 ,记这5件电器分别为a,b,c,d,e,其中”A”型为a,b.从中任选2件,所有可能的情况为ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种.
,记这5件电器分别为a,b,c,d,e,其中”A”型为a,b.从中任选2件,所有可能的情况为ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种.
其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd,be,共6种.所以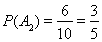 .
.
所以从重量在[80,85)的5件电器中,任选2件电器,其中恰有1件为”A”型的概率为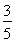 .
.
考点:1.概率的问题.2.通过列举分类的思想.3.审题能力的培养.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:大连市第八中学2006~2007学年度下学期期末考试高一数学试卷 题型:022
某电子元件厂对一批新产品(共100000件)的使用寿命进行检验,质检部分抽取容量为100的样本.经检测统计后,绘出了该产品的使用寿命的频率分布的直方图(如图所示),估计这批产品的使用寿命在400小时以上的产品件数约是________.

查看答案和解析>>
科目:高中数学 来源:2012年苏教版高数选修2-3 2.2超几何分布练习卷(解析版) 题型:选择题
一批产品共50件,次品率为4%,从中任取10件,则抽的1件次品的概率是
A.0.078 B.0.78 C.0.0078 D.0.078
查看答案和解析>>
科目:高中数学 来源:《3.2 函数模型及其应用》2013年同步练习(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com