Question

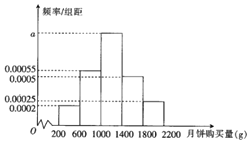
【题目】2018年中秋节到来之际，某超市为了解中秋节期间月饼的销售量，对其所在销售范围内的1000名消费者在中秋节期间的月饼购买量单位：进行了问卷调查，得到如下频率分布直方图：

求频率分布直方图中a的值；

以频率作为概率，试求消费者月饼购买量在的概率；

已知该超市所在销售范围内有20万人，并且该超市每年的销售份额约占该市场总量的，请根据这1000名消费者的人均月饼购买量估计该超市应准备多少吨月饼恰好能满足市场需求频率分布直方图中同一组的数据用该组区间的中点值作代表？

Answer 1

【答案】（1）；（2）0.62；（3）12.08吨

【解析】

（1）由频率分布直方图列出方程能求出a．

（2）由频率分布直方图先求出满足题意的频率，即得概率．

（3）由频率分布直方图先求出人均月饼购买量，由此能求出该超市应准备12.08吨月饼恰好能满足市场需求．

由，解得．

消费者月饼购买量在的频率为：

，

费者月饼购买量在的概率为．

由频率分布直方图得人均月饼购买量为：

，

∴万克吨，

∴该超市应准备吨月饼恰好能满足市场需求．