
在对人们休闲的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个 的列联表;
的列联表;
| P(k2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
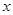 | 2 | 4 | 5 | 6 | 8 |
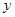 | 30 | 40 | 60 | 50 | 70 |
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
某校对高三年级的学生进行体检,现将高三男生的体重(单位:kg)数据进行整理后分成六组,并绘制频率分布直方图(如图).已知图中从左到右第一、第六小组的频率分别为0.16,0.07,第一、第二、第三小组的频率成等比数列,第三、第四、第五、第六小组的频率成等差数列,且第三小组的频数为100,则该校高三年级的男生总数为 
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| | 男 | 女 | 总计 |
| 走天桥 | 40 | 20 | |
| 走斑马线 | 20 | 30 | |
| 总计 | | | |
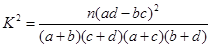 )
) | 0.050 0.010 0.001 |
 | 3.841 6.635 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
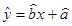 所表示的直线必经过的点;
所表示的直线必经过的点;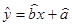 ;
;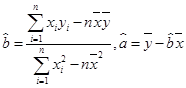 )
) 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校为了解毕业班学业水平考试学生的数学考试情况, 抽取了该校100名学生的数学成绩, 将所有数据整理后, 画出了样频率分布直方图(所图所示), 若第1组、第9组的频率各为 .
.
(Ⅰ) 求 的值, 并估计这次学业水平考试数学成绩的平均数;
的值, 并估计这次学业水平考试数学成绩的平均数;
(Ⅱ)若全校有1500名学生参加了此次考试,估计成绩在 分内的人数.
分内的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一600名学生进行了一次“钓鱼岛”
知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和
频率分布直方图.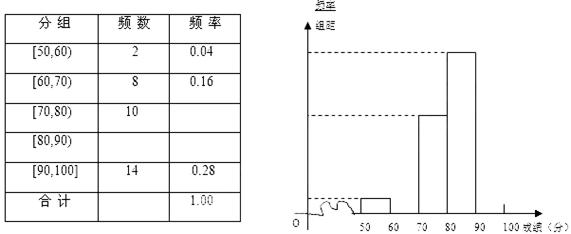
(1)填写答题卡频率分布表中的空格,补全频率分布直方图,并标出每个小矩形对应的纵轴数据;
(2)试估计该年段成绩在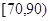 段的有多少人;
段的有多少人;
(3)请你估算该年级的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25 | [25,35 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 |  |  | |
| 不赞成 |  |  | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列。
的分布列。

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件?2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com