练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．设（x-$\frac{2}{\sqrt{x}}$）6的展开式中x3的系数为A，则A的值为（　　）
    A．60B．-60C．15D．-15

    分析 根据二项式展开式的通项公式，令x的指数等于3，即可求出展开式中x3的系数A．

    解答 解：（x-$\frac{2}{\sqrt{x}}$）6的展开式的通项公式为
    Tr+1=${C}_{6}^{r}$•x6-r•${（-\frac{2}{\sqrt{x}}）}^{r}$=（-2）r•${C}_{6}^{r}$•${x}^{6-\frac{3r}{2}}$，
    令6-$\frac{3r}{2}$=3，解得r=2，
    得展开式中x3的系数是
    A=（-2）2•${C}_{6}^{2}$=60．
    故选：A．

    点评 本题考查了利用二项式展开式的通项公式求特定项的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

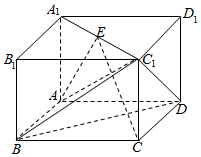    17．在长方体ABCD-A1B1C1D1中，E是A1C1与B1D1的交点，AB=BC=$\sqrt{2}$，AA1=1．
    （1）求证：AE∥平面C1BD；
    （2）求证：CE⊥平面C1BD；
    （3）求二面角A-BC1-D的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知a，b，c是三条不同的直线，α，β是两个不同的平面，给出下列命题：
    ①a?α，α∥β，则a∥β；
    ②若a∥α，α∥β，则a∥β；
    ③若α∥β，a⊥α，则a⊥β；
    ④若a∥β，a∩α=A，则a与β必相交；
    ⑤若异面直线a与b所成角为50°，b∥c，a与c异面，则a与c所成角为50°．
    其中正确命题的序号为①③④⑤．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若大前提是，任何实数的四次方都大于0，小前提是：a∈R，结论是：a4＞0，那么这个演绎推理（　　）
    A．大前提错误B．小前提错误C．推理形式错误D．没有错误

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若从高二男生中随机抽取5名男生，其身高和体重数据如表所示：
    身高x（cm）160165170175180
    体重y（kg）6366707477
    根据如表可得回归方程为：$\widehat{y}$=0.56x+$\widehat{a}$，则预报身高为172的男生的体重（　　）
    A．71.12B．约为71.12C．约为72D．无法预知

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设变量x，y满足约束条件$\left\{\begin{array}{l}{3x+y-6≥0}\\{x-y-2≤0}\\{y-3≤0}\end{array}\right.$，则$\frac{y+2}{x-2}$的取值范围是（　　）
    A．[-5，$\frac{5}{3}$]B．[-5，0）∪[$\frac{5}{3}$，+∞）C．（-∞，-5]∪[$\frac{5}{3}$，+∞）D．[-5，0）∪（0，$\frac{5}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知函数f（x）=$\sqrt{1-{x}^{2}}$，则${∫}_{-1}^{1}$ f （x）dx的值为（　　）
    A．$\frac{π}{4}$B．$\frac{π}{2}$C．πD．2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．计算：1-2sin2105°=（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{2}$C．-$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，则$\overrightarrow{a}$$•\overrightarrow{b}$+$\overrightarrow{b}$2=5．

    查看答案和解析>>

    同步练习册答案