
【题目】要得到函数y=3cos(2x﹣ ![]() )的图象,可以将函数y=3sin2x的图象( )
)的图象,可以将函数y=3sin2x的图象( )
A.沿x轴向左平移 ![]() 单位
单位
B.沿x轴向右平移 ![]() 单位
单位
C.沿x轴向左平移 ![]() 单位
单位
D.沿x轴向右平移 ![]() 单位
单位
【答案】A
【解析】解:∵函数 ![]() =3sin[
=3sin[ ![]() ﹣2x+
﹣2x+ ![]() ]=3sin(
]=3sin( ![]() ﹣2x)
﹣2x)
=﹣3sin(2x﹣ ![]() )=3sin(2x﹣
)=3sin(2x﹣ ![]() +π)=3sin(2x+
+π)=3sin(2x+ ![]() )=3sin[2(x+
)=3sin[2(x+ ![]() )],
)],
将函数y=3sin2x的图象沿x轴向左平移 ![]() 单位可得 y=3sin[2(x+
单位可得 y=3sin[2(x+ ![]() )]的图象,
)]的图象,
故选A.
【考点精析】通过灵活运用函数y=Asin(ωx+φ)的图象变换,掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象即可以解答此题.
的图象即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某消防机构为![]() 四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
小区 | A | B | C | D |
代表人数 | 45 | 60 | 30 | 15 |
(I)求此活动中各小区“幸运之星”的人数;
(II)从B小区和C小区的“幸运之星”中任选两人进行后续的活动,求这两个人均来自B小区的概率;
(III)消防机构在B小区内,对参加问答活动的居民进行了是否有兴趣参加消防安全培训的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过![]() 的前提下认为有兴趣参加消防安全培训与性别有关系?
的前提下认为有兴趣参加消防安全培训与性别有关系?
临界值表:
|
|
|
|
|
|
|
|
|
|
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 过点
过点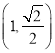 ,离心率为
,离心率为![]() ,
, ![]() ,
, ![]() 是椭圆
是椭圆![]() 的长轴的两个端点(
的长轴的两个端点(![]() 位于
位于![]() 右侧),
右侧),![]() 是椭圆在
是椭圆在![]() 轴正半轴上的顶点.
轴正半轴上的顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在经过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 和
和![]() ,使得向量
,使得向量![]() 与
与![]() 共线?如果存在,求出直线方程;如果不存在,请说明理由.
共线?如果存在,求出直线方程;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.
(1)证明:B﹣A= ![]() ;
;
(2)求sinA+sinC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人想参加《中国诗词大会》比赛,筹办方要从10首诗司中分别抽出3首让甲、乙背诵,规定至少背出其中2首才算合格; 在这10首诗词中,甲只能背出其中的7首,乙只能背出其中的8首
(1)求抽到甲能背诵的诗词的数量![]() 的分布列及数学期望;
的分布列及数学期望;
(2)求甲、乙两人中至少且有一人能合格的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com