
【题目】(1)已知直线方程为(2+m)x+(1-2m)y+4-3m=0,求证:不论m为何实数,此直线必过定点;
(2)过这定点引一直线,使它夹在两坐标轴间的线段被这点平分,求这条直线的方程.
【答案】(1)证明见解析;(2)2x+y+4=0
【解析】试题分析:(1)直线方程整理得m(x-2y-3)+2x+y+4=0,所以![]() ,求出定点;(2)由(-1,-2)是线段AB的中点,得到A(-2,0),B(0,-4),写出直线方程。
,求出定点;(2)由(-1,-2)是线段AB的中点,得到A(-2,0),B(0,-4),写出直线方程。
试题解析:
(1)证明:直线方程可写为m(x-2y-3)+2x+y+4=0,
由![]() ,得
,得![]() ,
,
∴点(-1,-2)适合方程(2+m)x+(1-2m)·y+4-3m=0,
因此,直线(2+m)x+(1-2m)y+4-3m=0过定点(-1,-2).
(2)设过点(-1,-2)所引的直线与x轴、y轴分别交于A(a,0),B(0,b)点,
∵(-1,-2)是线段AB的中点,
∴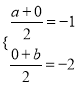 ,解得
,解得![]()
∴所求直线方程为![]() ,即2x+y+4=0.
,即2x+y+4=0.


科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
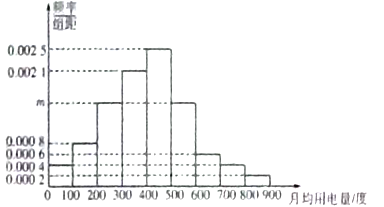
(Ⅰ)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆![]() 上每一点的纵坐标不变,横坐标变为原来的
上每一点的纵坐标不变,横坐标变为原来的![]() ,得曲线C.
,得曲线C.
(Ⅰ)写出C的参数方程;
(Ⅱ)设直线l: ![]() 与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1 P2的中点且与l垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟投资100万元,有两种投资方案可供选择:一种是年利率为10%,按单利计算,5年后收回本金和利息;另一种是年利率为9%,按每年复利一次计算,5年后收回本金和利息.哪一种投资更有利?这种投资比另一种投资5年可多得利息多少元?(结果精确到0.01万元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)=![]() t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有4位同学在同一天的上午、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学测试两个项目,分别在上午和下午,且每人上午和下午测试的项目不能相同.若上午不测“握力”,下午不测“台阶”,其余项目上午、下午都各测试一人,则不同的安排方式的种数为( )
A. 264 B. 72 C. 266 D. 274
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都乘以同一个非零常数![]() 后,标准差也变为原来的
后,标准差也变为原来的![]() 倍;
倍;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时, ![]() 平均减少5个单位;
平均减少5个单位;
③线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
④在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() ,若
,若![]() 位于区域
位于区域![]() 的概率为0.4,则
的概率为0.4,则![]() 位于区域
位于区域![]() 内的概率为0.6
内的概率为0.6
⑤利用统计量![]() 来判断“两个事件
来判断“两个事件![]() 的关系”时,算出的
的关系”时,算出的![]() 值越大,判断“
值越大,判断“![]() 与
与![]() 有关”的把握就越大
有关”的把握就越大
其中正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com