练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    对函数f(x)＝1－(x∈R)的如下研究结果，正确的是         (　　)

    A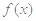．既不是奇函数又不是偶函数．

    B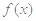．既是奇函数又是偶函数．

    C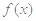．是偶函数但不是奇函数．

    D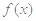．是奇函数但不是偶函数．

     

    【答案】

    D

    【解析】

    试题分析：要说明一个函数是奇函数（或偶函数）必须根据定义证明，而要说明它不是奇函数（或偶函数）可举特例说明），

    考点：函数的奇偶性.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：013

    对函数f(x)＝3x4＋4x3－12x2＋15，给出命题：

    ①f(x)的极小值只有f(－2)＝－17，f(1)＝10，极大值为f(0)＝15

    ②f(x)的极小值只有f(－1)＝2，f(1)＝10，极大值为f(0)＝15．

    ③f(x)极大值为f(2)＝47，极小值f(0)＝15，f(－2)＝－17

    ④极大值为f(－2)＝－17，f(1)＝10，极小值为f(－1)＝2其中正确命题的个数为

    [　　]

    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    科目：高中数学 来源：山东省聊城市2007年高考模拟试题数学理科 题型：013

    对函数F(x)＝｜sinx｜＋sin｜x｜的性质的描述：①函数图象关于原点对称；②函数图象关于y轴对称；③该函数既有最大值又有最小值．其中正确的个数为

    [　　]

    A．3

    B．2

    C．1

    D．0

    查看答案和解析>>

    科目：高中数学 来源：重庆西南师大附中2011届高三第一次月考理科数学试题 题型：044

    定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M＞0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．

    已知函数f(x)＝1＋a·x＋x；g(x)＝．

    (1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；

    (2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围；

    (3)若m＞0，函数g(x)在[0，1]上的上界是T(m)，求T(m)的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝.

    (1)求函数f(x)的单调区间和极值；

    (2)若函数y＝g(x)对任意x满足g(x)＝f(4－x)，求证：当x>2，f(x)>g(x)；

    (3)若x1≠x2，且f(x1)＝f(x2)，求证：x1＋x2>4.

    查看答案和解析>>

    同步练习册答案