
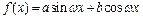 (
( R,且
R,且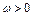 )的部分图象如图所示.
)的部分图象如图所示.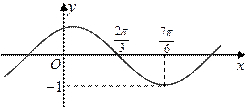
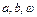 的值;
的值;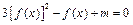
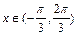 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围. ,
, (2) m的取值范围是:
(2) m的取值范围是: 或
或
 的周期为
的周期为 (
(

 )=
)= ,∴
,∴ .
. 且
且 , 即
, 即 , 解得:
, 解得:  . 所以,
. 所以,
 . [也可以按以下解释: 上述函数的图象可由
. [也可以按以下解释: 上述函数的图象可由 的图象沿
的图象沿 轴负方向平移
轴负方向平移 个单位而得到,∴其解析式为
个单位而得到,∴其解析式为 .∴
.∴
 ∴
∴ ,∴
,∴ .设
.设 ,
, 在(0,1)仅有一根或有两个相等的根.
在(0,1)仅有一根或有两个相等的根.  时,y =
时,y = ;t = 0时,y = 0;t = 1时,y = 2.
;t = 0时,y = 0;t = 1时,y = 2.  或0≤-m<2时,直线l与曲线C有且只有一个公共点.
或0≤-m<2时,直线l与曲线C有且只有一个公共点. 或
或
 仅有一根在(0, 1)时,令
仅有一根在(0, 1)时,令 则
则 得到
得到 ; 或
; 或 时
时 ,或
,或 时
时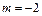 (舍去)
(舍去)  ,
,
 或
或


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com