
| 温度x(℃) | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
分析 (1)由总数除以天数得平均数,根据方差公式,代入可得方差;
(2)根据公式求回归系数,可得回归方程;x=30,代入计算,可预测当温度为30℃时所卖西瓜的个数.
解答 解:(1)$\overline{y}$=$\frac{20+22+24+30+34}{5}$=26,
方差为s2=$\frac{1}{5}×$[(20-26)2+(22-26)2+(24-26)2+(30-26)2+(34-26)2]=27.2.
(2)$\overline{x}$=35,$\sum_{i=1}^{5}{{x}_{i}}^{2}$=6151,$\sum_{i=1}^{5}{x}_{i}{y}_{i}$=4608,
所以$\stackrel{∧}{b}$=$\frac{4608-5×35×26}{6151-5×3{5}^{2}}$≈2.2,$\stackrel{∧}{a}$=25-2.2×35=-51,
所以回归直线方程为$\stackrel{∧}{y}$=2.2x-51,
当x=30时,$\stackrel{∧}{y}$=15,所以预测当温度为30℃时所卖西瓜的个数为15.
点评 本题考查平均值和方差,考查线性回归方程,正确计算是关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
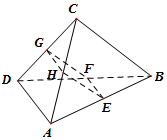 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${P}_{8}^{2}$${P}_{6}^{2}$${P}_{4}^{2}$${P}_{2}^{2}$ | B. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$ | ||
| C. | ${C}_{8}^{2}$${C}_{6}^{2}$${C}_{4}^{2}$${C}_{2}^{2}$${P}_{4}^{4}$ | D. | $\frac{C_8^2C_6^2C_4^2C_2^2}{4!}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com