练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图,已知平面α∩β=a,　bβ,a∩b=A,且cα,c∥a,求证:b、c为异面直线.?

    ?

          

    思路分析:反证法.假设b、c共面,则有两种情况:①b与c相交;②b与c平行.?

           证法一:假设b、c不是异面直线,即b、c为共面直线,则b、c为相交直线或平行直线.

           (1)若b∩c=P,已知bβ,cα,又α∩β=a,则P∈bβ,且P∈cα,从而,交点P一定在平面α、β的交线上(公理二),即P∈a,于是a∩c=P,这与已知条件a∥c矛盾.因此b、c相交不成立.?

           (2)若b∥c,已知a∥c,则a∥b(公理四),这与已知条件a∩b=A矛盾,因此b、c平行也不能成立.?

           综合(1)(2)可知b、c为异面直线.?

           证法二:假设b、c不是异面直线,即假设直线b、c在同一个平面γ内,则b γ,cγ,在直线b上任取一点B(不同于A,B α);从而,平面γ一定经过B点与直线c.?

           又∵A∈a,a∥c,?

           ∴Aα.于是c与c外一点A的平面就是α,而这样的平面只能有一个.从而,直线b、c都在平面α内,但B∈bα,这与Bα矛盾.因此b、c为异面直线.?

           温馨提示:立体几何中异面直线问题、共面问题常用反证法.反证法中要正确推理,将反设列入已知条件,按一般逻辑推理程序和法则推理.推理中没有用到“反设”就不是反证法.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：重难点手册　高中数学·必修4（配人教A版新课标） 人教A版新课标 题型：044

    如下图，已知平面上三点坐标分别为A(－2，1)，B(－1，3)，C(3，4)．求D的坐标，使得这四点构成一个平行四边形．

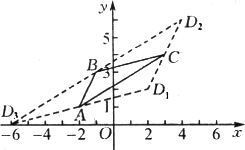
    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：047

    如下图，已知平面α⊥平面γ，平面β⊥平面γ．α∩γ＝a，β∩γ＝b且a∥b，求证α∥β．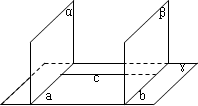

    查看答案和解析>>

    科目：高中数学 来源：湖北省荆州中学2008高考复习立体几何基础题题库一(有详细答案)人教版 人教版 题型：047

    如下图，已知平面α∥平面β，A、C∈α，B、D∈β，E、F分别为AB、CD的中点．求证：EF∥α，EF∥β．

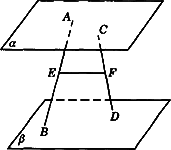
    查看答案和解析>>

    科目：高中数学 来源：导学大课堂必修二数学苏教版 苏教版 题型：022

    如下图，已知平面α∥β∥γ，两条直线l、m分别与平面α、β、γ相交于点A、B、C与点D、E、F．已知AB＝6，而，则AC＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：044

    如下图，已知平面，，且，，，，是垂足，试判断直线与的位置关系？并证明你的结论．

    查看答案和解析>>

    同步练习册答案