
【题目】已知函数![]() 是二次函数,不等式
是二次函数,不等式![]() 的解集为
的解集为![]() ,且
,且![]() 在区间
在区间![]() 上的最小值是4.
上的最小值是4.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 在
在![]() 上的最大值
上的最大值![]() 、最小值
、最小值![]() 的解析式;
的解析式;
(3)设![]() ,若对任意
,若对任意![]() 均成立,求实数
均成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数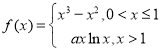 ,(
,(![]() ).
).
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)设点![]() ,
,![]() 是函数
是函数![]() 图象的不同两点,其中
图象的不同两点,其中![]() ,
,![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() ,且函数
,且函数![]() 在点
在点![]() 切线的斜率为
切线的斜率为![]() ,若存在,请求出
,若存在,请求出![]() 的范围;若不存在,请说明理由.
的范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图(如图)和B地区用户满意度评分的频数分布表.

B地区用户满意度评分的频数分布表
满意度评分分组 |
|
|
|
|
|
频数 | 2 | 8 | 14 | 10 | 6 |
在图中作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组为了研究昼夜温差对一种稻谷种子发芽情况的影响,他们分别记录了4月1日至4月5日的每天星夜温差与实验室每天每100颗种子的发芽数,得到如下资料:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 |
温差 | 9 | 10 | 11 | 8 | 12 |
发芽数 | 38 | 30 | 24 | 41 | 17 |
利用散点图,可知![]() 线性相关。
线性相关。
(1)求出![]() 关于
关于![]() 的线性回归方程,若4月6日星夜温差
的线性回归方程,若4月6日星夜温差![]() ,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
,请根据你求得的线性同归方程预测4月6日这一天实验室每100颗种子中发芽颗数;
(2)若从4月1日![]() 4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
4月5日的五组实验数据中选取2组数据,求这两组恰好是不相邻两天数据的概率.
(公式: )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某文体局为了解“跑团”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期间“跑团”每月跑步的平均里程(单位:公里)的数据,绘制了下面的折线图.根据折线图,下列结论正确的是( )

A. 月跑步平均里程的中位数为6月份对应的里程数
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相对于6月至11月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .将
.将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数![]() ,下列命题正确的是( )
,下列命题正确的是( )
A. 函数![]() 在区间
在区间![]() 上有最小值 B. 函数
上有最小值 B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 的一条对称轴为
的一条对称轴为![]() D. 函数
D. 函数![]() 的一个对称点为
的一个对称点为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付酬方案:
第一种,每天支付![]() 元,没有奖金;
元,没有奖金;
第二种,每天的底薪![]() 元,另有奖金.第一天奖金
元,另有奖金.第一天奖金![]() 元,以后每天支付的薪酬中奖金比前一天的奖金多
元,以后每天支付的薪酬中奖金比前一天的奖金多![]() 元;
元;
第三种,每天无底薪,只有奖金.第一天奖金![]() 元,以后每天支付的奖金是前一天的奖金的
元,以后每天支付的奖金是前一天的奖金的![]() 倍.
倍.
(1)工作![]() 天
天![]() ,记三种付费方式薪酬总金额依次为
,记三种付费方式薪酬总金额依次为![]() 、
、![]() 、
、![]() ,写出
,写出![]() 、
、![]() 、
、![]() 关于
关于![]() 的表达式;
的表达式;
(2)该学生在暑假期间共工作![]() 天,他会选择哪种付酬方式?
天,他会选择哪种付酬方式?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民节能环保意识,某市面向全市征召义务宣传志愿者,现从符合条件的500名志愿者中随机抽取100名志愿者,他们的年龄情况如下表所示:
分组(单位:岁) | 频数 | 频率 |
| 5 | 0.05 |
| ① | 0.20 |
| 35 | ② |
| 30 | 0.30 |
| 10 | 0.10 |
总计 | 100 | 1.00 |

(1)频率分布表中的①②位置应填什么数据?
(2)补全如图所示的频率分布直方图,再根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数.
岁的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com