
【题目】在直角坐标系x-O-y中,已知曲线E:![]() (t为参数)
(t为参数)
(1)在极坐标系O-x中,若A、B、C为E上按逆时针排列的三个点,△ABC为正三角形,其中A点的极角θ=![]() ,求B、C两点的极坐标;
,求B、C两点的极坐标;
(2)在直角坐标系x-O-y中,已知动点P,Q都在曲线E上,对应参数分别为t=α与t=2α (0<α<2π),M为PQ的中点,求 |MO| 的取值范围
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图3是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
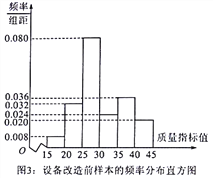
表1:设备改造后样本的频数分布表

(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;

(2)根据图3和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)企业将不合格品全部销毁后,根据客户需求对合格品进行等级细分,质量指标值落在![]() 内的定为一等品,每件售价240元;质量指标值落在
内的定为一等品,每件售价240元;质量指标值落在![]() 或
或![]() 内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为
内的定为二等品,每件售价180元;其它的合格品定为三等品,每件售价120元.根据表1的数据,用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品,设其支付的费用为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望.
的分布列和数学期望.
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
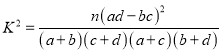
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,试探究:直线
,试探究:直线![]() 是否过定点,若是,求该定点的坐标,若不是,请说明.
是否过定点,若是,求该定点的坐标,若不是,请说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点
的中点
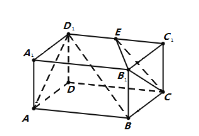
(1)在所给图中画出平面![]() 与平面
与平面![]() 的交线(不必说明理由)
的交线(不必说明理由)
(2)证明:![]() 平面
平面![]()
(3)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() .
.
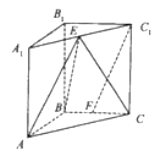
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若直线![]() 和平面
和平面![]() 所成角的正弦值等于
所成角的正弦值等于![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告.已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如下表所示:
连续剧 | 连续剧播放时长/min | 广告播放时长/min | 收视人次/万人 |
甲 | 70 | 5 | 60 |
乙 | 60 | 5 | 25 |
电视台每周安排的甲、乙连续剧的总播放时长不多于![]() ,广告的总播放时长不少于
,广告的总播放时长不少于![]() ,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用
,且甲连续剧播放的次数不多于乙连续剧播放次数的2倍,分别用![]() ,
,![]() 表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为( )
表示每周计划播出的甲、乙两套连续剧的次数,要使总收视人次最多,则电视台每周播出甲、乙两套连续剧的次数分别为( )
A.6,3B.5,2C.4,5D.2,7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com