
【题目】在直角坐标系![]() 中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() ,过点
,过点![]() 的直线l的参数方程为
的直线l的参数方程为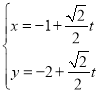 (t为参数),l与C交于A,B两点.
(t为参数),l与C交于A,B两点.
(1)求C的直角坐标方程和l的普通方程;
(2)若![]() ,
,![]() ,
,![]() 成等比数列,求a的值.
成等比数列,求a的值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】英国统计学家E.H.辛普森1951年提出了著名的辛普森悖论,下面这个案例可以让我们感受到这个悖论.有甲乙两名法官,他们都在民事庭和行政庭主持审理案件,他们审理的部分案件被提出上诉.记录这些被上述案件的终审结果如下表所示(单位:件):
法官甲 | 法官乙 | ||||||
终审结果 | 民事庭 | 行政庭 | 合计 | 终审结果 | 民事庭 | 行政庭 | 合计 |
维持 | 29 | 100 | 129 | 维持 | 90 | 20 | 110 |
推翻 | 3 | 18 | 21 | 推翻 | 10 | 5 | 15 |
合计 | 32 | 118 | 150 | 合计 | 100 | 25 | 125 |
记甲法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为
,记乙法官在民事庭、行政庭以及所有审理的案件被维持原判的比率分别为![]() ,
,![]() 和
和![]() ,则下面说法正确的是
,则下面说法正确的是
A. ![]() ,
,![]() ,
,![]() B.
B. ![]() ,
,![]() ,
,![]()
C. ![]() ,
,![]() ,
,![]() D.
D. ![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司新开发一电子产品,该电子产品的一个系统G有3个电子元件组成,各个电子元件能否正常工作的概率均为![]() ,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
,且每个电子元件能否正常工作相互独立.若系统C中有超过一半的电子元件正常工作,则G可以正常工作,否则就需要维修,且维修所需费用为500元.
(1)求系统不需要维修的概率;
(2)该电子产品共由3个系统G组成,设E为电子产品需要维修的系统所需的费用,求![]() 的分布列与期望;
的分布列与期望;
(3)为提高G系统正常工作概率,在系统内增加两个功能完全一样的其他品牌的电子元件,每个新元件正常工作的概率均为![]() ,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:
,且新增元件后有超过一半的电子元件正常工作,则C可以正常工作,问:![]() 满足什么条件时,可以提高整个G系统的正常工作概率?
满足什么条件时,可以提高整个G系统的正常工作概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,大量的统计数据表明,参与调查者中关注此问题的约占80%.现从参与调查的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第1组
人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4 组
,第4 组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示
,得到的频率分布直方图如图所示
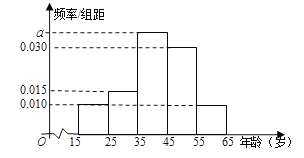
(1) 求![]() 的值
的值
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行问卷调查,求在第1组已被抽到
人进行问卷调查,求在第1组已被抽到![]() 人的前提下,第3组被抽到
人的前提下,第3组被抽到![]() 人的概率;
人的概率;
(3)若从所有参与调查的人中任意选出![]() 人,记关注“生态文明”的人数为
人,记关注“生态文明”的人数为![]() ,求
,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某社区举行的2020迎春晚会上,张明和王慧夫妻俩参加该社区的“夫妻蒙眼击鼓”游戏,每轮游戏中张明和王慧各蒙眼击鼓一次,每个人击中鼓则得积分100分,没有击中鼓则扣积分50分,最终积分以家庭为单位计分.已知张明每次击中鼓的概率为![]() ,王慧每次击中鼓的概率为
,王慧每次击中鼓的概率为![]() ;每轮游戏中张明和王慧击中与否互不影响,假设张明和王慧他们家庭参加两轮蒙眼击鼓游戏.
;每轮游戏中张明和王慧击中与否互不影响,假设张明和王慧他们家庭参加两轮蒙眼击鼓游戏.
(1)若家庭最终积分超过200分时,这个家庭就可以领取一台全自动洗衣机,问张明和王慧他们家庭可以领取一台全自动洗衣机的概率是多少?
(2)张明和王慧他们家庭两轮游戏得积分之和![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)a≥-2时,求F(x)=f(x)-g(x)的单调区间;
(2)设h(x)=f(x)+g(x),且h(x)有两个极值点为![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com