
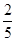 ,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ.
,(Ⅰ)求n;(Ⅱ)从袋中不放回的依次摸出三个球,记ξ为相邻两次摸出的球不同色的次数(例如:若取出的球依次为红球、白球、白球,则ξ=1),求随机变量ξ的分布列及其数学期望Eξ. 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
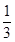 ,将赝品错误地鉴定为正品的概率为
,将赝品错误地鉴定为正品的概率为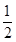 ,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数
,已知一批物品共有4件,其中正品3件,赝品1件.(1)求该收藏爱好者的鉴定结果为正品2件,赝品2件的概率;(2)求该收藏爱好者的鉴定结果中正品数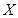 的分布列及数学期望.
的分布列及数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
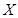 为选出的4名选手中女选手的人数,求
为选出的4名选手中女选手的人数,求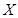 的分布列和期望.
的分布列和期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
甲部门不同岗位月工资 (元) (元) | 2200 | 2400 | 2600 | 2800 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
乙部门不同岗位月工资 (元) (元) | 2000 | 2400 | 2800 | 3200 |
获得相应岗位的概率 | 0.4 | 0.3 | 0.2 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com