练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设随机变量具有分布P（=k）=，k=1，2，3，4，5，求E（+2）2，V（2-1），（-1）.
    E（+2）2=3，V（2-1）=2，（-1）=.
    ∵E（）=1×+2×+3×+4×+5×=3.
    E（2）=1×+22×+32×+42×+52×=11.
    V（)=（1-3）2×+（2-3）2×+（3-3）2×+（4-3）2×+（5-3）2×
    =（4+1+0+1+4）="2.                                              " 5分
    ∴E（+2）2=E（2+4+4）
    =E(2)+4E()+4="11+12+4=27.                                      " 8分
    V（2-1）=4V()=8，                                                      11分
    （-1）===.                                             14分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某城市有甲、乙、丙、丁4个旅游景点，一位客人游览这4个景点的概率都是0.6，且客人是否游览哪个景点互不影响．设表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．
    （1）求的分布列及数学期望；
    （2）记“函数在区间上单调递增”为事件A，求事件A的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本上题满分12分）某高校为了参加“CBA杯”安徽省大学生篮球联赛暨第十届CU—BA安徽省选拔赛，需要在各班选拔预备队员，规定投篮成绩甲级的可作为入围选手，选拔过程中每人投篮5次，若投中3次则确定为乙级，若投中4次及以上则可确定为甲级，一旦投中4次，即终止投篮，已知某班同学小明每次投篮投中的概率是0.6。（I）求小明投篮4次才被确定为乙级的概率； （II）设小明投篮投中次数为X，求X的分布列及期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    射击运动员在双项飞碟比赛中，每轮比赛连续发射两枪，击中两个飞靶得2分，击中一个飞靶得1分，不击中飞靶得0分，某射击运动员在每轮比赛连续发射两枪时，第一枪命中率为，第二枪命中率为，该运动员如进行2轮比赛．
    （Ⅰ）求该运动员得4分的概率为多少？
    （Ⅱ）若该运动员所得分数为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在2008年春运期间，一名大学生要从广州回到郑州老家有两种选择，即坐火车或汽车。已知该大学生先去买火车票的概率是先去买汽车票概率的3倍，汽车票随时都能买到。若先去买火车票，则买到火车票的概率为0.6，买不到火车票，再去买汽车票。
    （I）求这名大学生先去买火车票的概率；
    （II）若火车票的价格为120元，汽车票的价格为280元，设该大学生购买车票所花费钱数为的期望值。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不返回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量为此时已摸球的次数，求：
    (1)随机变量的概率分布列；(2)随机变量的数学期望与方差.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某公司“咨询热线”电话共有8路外线，经长期统计发现，在8点到10点这段时间内，外线电话同时打入情况如下表所示：
    电话同时
    打入个数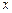
    		0
    		1
    		2
    		3
    		4
    		5
    		6
    		7
    		8
    概率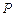
    		0．13
    		0．35
    		0．27
    		0．14
    		0．08
    		0．02
    		0．01
    		0
    		0
    （1）若这段时间内，公司只安排了2位接线员（一个接线员一次只能接一个电话）
    ①求至少一路电话不能一次接通的概率；
    ②在一周五个工作日中，如果有三个工作日的这段时间（8点至10点）内至少一路电话不能一次接通，那么公司的形象将受到损害，现用至少一路电话不能一次接通的概率表示公司形象的“损害度”，求上述情况下公司形象的“损害度”．
    （2）求一周五个工作日的这段时间（8点至10点）内，电话同时打入数X的均值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    从集合的所有非空子集中，等可能地取出一个.
    （理）记所取出的非空子集中元素的个数为，则的数学期望=       .
    （文）取出的非空子集中所有元素之和恰为6的概率=       .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设是随机变量，且，则 (     ) ．
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案