
【题目】如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上.
上.
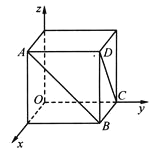
(1)当![]() ,且点
,且点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() 时,求
时,求![]() 的长度;
的长度;
(2)当点![]() 是面对角线
是面对角线![]() 的中点,点
的中点,点![]() 在面对角线
在面对角线![]() 上运动时,探究
上运动时,探究![]() 的最小值.
的最小值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知点P在曲线x2+y2=1上运动,过点P作x轴的垂线,垂足为Q,动点M满足![]() .
.
(1)求动点M的轨迹方程;
(2)点AB在直线x﹣y﹣4=0上,且AB=4,求△MAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() (a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足
(a>b>0)的右焦点为F,椭圆C上的两点A,B关于原点对称,且满足![]() ,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
,|FB|≤|FA|≤2|FB|,则椭圆C的离心率的取值范围是( )
A. B.
B.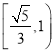
C.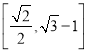 D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数![]() 是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数
是检测空气质量的重要参数,其数值越大说明空气污染状况越严重,空气质量越差.某地环保部门统计了该地区某月1日至24日连续24天的空气质量指数![]() ,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
,根据得到的数据绘制出如图所示的折线图,则下列说法错误的是( )
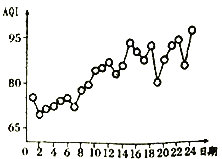
A. 该地区在该月2日空气质量最好
B. 该地区在该月24日空气质量最差
C. 该地区从该月7日到12日![]() 持续增大
持续增大
D. 该地区的空气质量指数![]() 与这段日期成负相关
与这段日期成负相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣1=0与直线x﹣2y+1=0交于点P.
(Ⅰ)求过点P且平行于直线3x+4y﹣15=0的直线![]() 的方程;(结果写成直线方程的一般式)
的方程;(结果写成直线方程的一般式)
(Ⅱ)求过点P并且在两坐标轴上截距相等的直线![]() 方程(结果写成直线方程的一般式)
方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 个人排成一排,在下列情况下,各有多少种不同排法?
个人排成一排,在下列情况下,各有多少种不同排法?
(1)甲不在两端;
(2)甲、乙、丙三个必须在一起;
(3)甲、乙必须在一起,且甲、乙都不能与丙相邻.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com