
【题目】一直函数![]() ,其中
,其中![]()
(1)讨论![]() 的单调性
的单调性
(2)设曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,曲线在点
,曲线在点![]() 处的切线方程为
处的切线方程为![]() ,求证:对于任意的正实数
,求证:对于任意的正实数![]() ,都有
,都有![]()
(3)若关于![]() 的方程
的方程![]() (
(![]() 为实数)有两个正实根
为实数)有两个正实根![]() ,求证:
,求证:![]()
【答案】
(1)
当![]() 为奇数时,
为奇数时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 内单调递增;当
内单调递增;当![]() 为偶数时,
为偶数时,![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减1
上单调递减1
(2)
见解答
(3)
见解答
【解析】(1)由![]() ,可得,其中
,可得,其中![]() 且
且![]() ,下面分两种情况讨论:当
,下面分两种情况讨论:当![]() 为奇数时:令
为奇数时:令![]() ,解得
,解得![]() 或
或![]() ,当
,当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
x | (- | (-1,1) | (1,+ |
F’(x) | — | + | — |
F(x) |
|
|
|
所以,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 内单调递增;当
内单调递增;当![]() 为偶数时,当
为偶数时,当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递增;当
单调递增;当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减,所以,
单调递减,所以,![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减
上单调递减
(2)证明:设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ,令
,令![]() ,即
,即![]() ,则
,则![]() 由于
由于![]() 在
在![]() 上单调递增,故
上单调递增,故![]() 在
在![]() 上单调递减,又因为
上单调递减,又因为![]() ,所以,当
,所以,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,所以对任意的正实数
内单调递减,所以对任意的正实数![]() 都有
都有![]() ,即对任意的正实数
,即对任意的正实数![]() ,都有
,都有![]()
(3)证明:不妨设![]() ,由(2)知
,由(2)知![]() ,设方程
,设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上单调递减,又由(2)知
上单调递减,又由(2)知![]() ,可得
,可得![]() 。类似的,设曲线
。类似的,设曲线![]() 在原点处的切线方程为
在原点处的切线方程为![]() ,可得
,可得![]() ,当
,当![]() ,
,![]() ,即对任意
,即对任意![]() 。设方程
。设方程![]() 的根为
的根为![]() ,可得
,可得![]() ,因为
,因为![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 因此
因此![]() .由此可得
.由此可得![]() ,因为
,因为![]() ,所以
,所以![]() ,故
,故![]() ,所以
,所以![]()
【考点精析】认真审题,首先需要了解导数的几何意义(通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ),还要掌握基本求导法则(若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导)的相关知识才是答题的关键.
),还要掌握基本求导法则(若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导)的相关知识才是答题的关键.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】(2015·陕西)设fn(x)=x+x2+x...+xn-1, n![]() N, n≥2。
N, n≥2。
(1)fn'(2)
(2)证明:fn(x)在(0,![]() )内有且仅有一个零点(记为an), 且0<an-
)内有且仅有一个零点(记为an), 且0<an-![]() <
<![]() (
(![]() )n.
)n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若关于![]() 的方程
的方程![]() 的解集中恰有一个元素,求
的解集中恰有一个元素,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,函数
,函数![]() 在区间
在区间![]() 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥P-ABC中,PA![]() 平面ABC,
平面ABC,![]()

(1)(Ⅰ)求三棱锥P-ABC的体积;
(2)(Ⅱ)证明:在线段PC上存在点M,使得AC![]() BM,并求
BM,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() ,过点D(1,0)且不过点E(2,1)的直线与椭圆C交于A,B两点,直线AE与直线x=3交于点M。
,过点D(1,0)且不过点E(2,1)的直线与椭圆C交于A,B两点,直线AE与直线x=3交于点M。
(1)(I)求椭圆C的离心率;
(2)(II)若AB垂直于x轴,求直线BM的斜率。
(3)(III)试判断直线BM与直线DE的位置关系,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额
(单位:万元)都在区间![]() 内,其频率分布直方图如图所示.
内,其频率分布直方图如图所示.
(Ⅰ)直方图中的![]() ;
;
(Ⅱ)在这些购物者中,消费金额在区间![]() 内的购物者的人数为 .
内的购物者的人数为 . 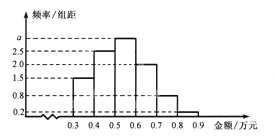
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(2015·重庆)如题(21)图,椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() 且过
且过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,
两点,
且![]() 。
。
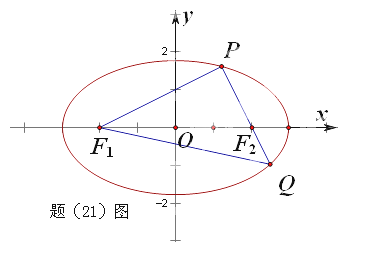
(1)若![]() 求椭圆的标准方程。
求椭圆的标准方程。
(2)若![]() ,且
,且![]() ,试确定椭圆离心率的取值范围。
,试确定椭圆离心率的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)设某校新、老校区之间开车单程所需时间为T,T只与道路畅通状况有关,对其容量为100的样本进行统计,结果如下:
T(分钟) | 25 | 30 | 35 | 40 |
频数(次) | 20 | 30 | 40 | 10 |
(1)求T的分布列与数学期望ET;
(2)刘教授驾车从老校区出发,前往新校区做一个50分钟的讲座,结束后立即返回老校区,求刘教授从离开老校区到返回老校区共用时间不超过120分钟的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com