
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() 是大于0的常数).以坐标原点为极点,
是大于0的常数).以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的极坐标方程和圆
的极坐标方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)分别记直线![]() :
: ![]() ,
, ![]() 与圆
与圆![]() 、圆
、圆![]() 的异于原点的焦点为
的异于原点的焦点为![]() ,
, ![]() ,若圆
,若圆![]() 与圆
与圆![]() 外切,试求实数
外切,试求实数![]() 的值及线段
的值及线段![]() 的长.
的长.
【答案】(1) ![]() ,
, ![]() (2)
(2) ![]() ,
, ![]()
【解析】试题分析:(1)先将圆![]() 的参数方程化为直角坐标方程,再利用
的参数方程化为直角坐标方程,再利用![]() 可得圆
可得圆![]() 的极坐标方程,两边同乘以
的极坐标方程,两边同乘以![]() 利用互化公式 即可得圆
利用互化公式 即可得圆![]() 的直角坐标方程;(2)由(1)知圆
的直角坐标方程;(2)由(1)知圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ;圆
;圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
, ![]() 圆
圆![]() 与圆
与圆![]() 外切的性质列方程解得
外切的性质列方程解得![]() ,分别将
,分别将![]() 代入
代入![]() 、
、![]() 的极坐标方程,利用极径的几何意义可得线段
的极坐标方程,利用极径的几何意义可得线段![]() 的长.
的长.
试题解析:(1)圆![]() :
: ![]() (
(![]() 是参数)消去参数
是参数)消去参数![]() ,
,
得其普通方程为![]() ,
,
将![]() ,
, ![]() 代入上式并化简,
代入上式并化简,
得圆![]() 的极坐标方程
的极坐标方程![]() ,
,
由圆![]() 的极坐标方程
的极坐标方程![]() ,得
,得![]() .
.
将![]() ,
, ![]() ,
, ![]() 代入上式,
代入上式,
得圆![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由(1)知圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ;圆
;圆![]() 的圆心
的圆心![]() ,半径
,半径![]() ,
,
![]() ,
,
∵圆![]() 与圆
与圆![]() 外切,
外切,
∴![]() ,解得
,解得![]() ,
,
即圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,得
,得![]() ;
;
将![]() 代入
代入![]() ,得
,得![]() ,得
,得![]() ;
;
故![]() .
.


科目:高中数学 来源: 题型:
【题目】共享单车是指企业的校园,地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是一种分时租赁模式,某共享单车企业为更好服务社会,随机调查了100人,统计了这100人每日平均骑行共享单车的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知骑行时间在![]() 三组对应的人数依次成等差数列
三组对应的人数依次成等差数列
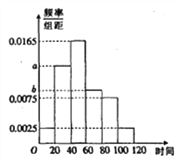
(1)求频率分布直方图中![]() 的值.
的值.
(2)若将日平均骑行时间不少于80分钟的用户定义为“忠实用户”,将日平均骑行时间少于40分钟的用户为“潜力用户”,现从上述“忠实用户”与“潜力用户”的人中按分层抽样选出5人,再从这5人中任取3人,求恰好1人为“忠实用户”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( )
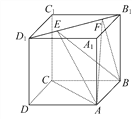
A. AC⊥BE
B. EF∥平面ABCD
C. 三棱锥A-BEF的体积为定值
D. △AEF的面积与△BEF的面积相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-![]() 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(1)当a=1时,求函数y=f(x)的值域;
(2)求函数y=f(x)在区间(0,1]上的最大值及最小值,并求出当函数f(x)取得最值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() 是等边三角形.
是等边三角形.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)点![]() 在椭圆
在椭圆![]() 上,线段
上,线段![]() 与线段
与线段![]() 交于点
交于点![]() ,若
,若![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com