
【题目】已知圆x2+y2+x﹣6y+m=0和直线x+2y﹣3=0交于P、Q两点,
(1)求实数m的取值范围;
(2)求以PQ为直径且过坐标原点的圆的方程.
【答案】
(1)解:圆x2+y2+x﹣6y+m=0,可化为(x+ ![]() )2+(y﹣3)2=﹣m+
)2+(y﹣3)2=﹣m+ ![]() ,
,
∴ ![]() <
< ![]() ,
,
∴﹣m+ ![]() >
> ![]() ,
,
∴m<8;
(2)解:设P(x1,y1),Q(x2,y2),
由题意得:OP、OQ所在直线互相垂直,则kOPkOQ=﹣1,∴x1x2+y1y2=0,
又因为x1=3﹣2y1,x2=3﹣2y2,
所以(3﹣2y1)(3﹣2y2)+y1y2=0,即5y1y2﹣6(y1+y2)+9=0①,
将直线l的方程:x=3﹣2y代入圆的方程得:5y2﹣20y+12+m=0,
所以y1+y2=4,y1y2= ![]() ,
,
代入①式得:5× ![]() ﹣6×4+9=0,解得m=3,
﹣6×4+9=0,解得m=3,
故实数m的值为3
【解析】(1)利用圆心到直线的距离小于半径,即可求实数m的取值范围;(2)设点P(x1 , y1),Q(x2 , y2),由题意得OP、OQ所在直线互相垂直,即kOPkOQ=﹣1,亦即x1x2+y1y2=0,根据P、Q在直线l上可变为关于y1、y2的表达式,联立直线方程、圆的方程,消掉x后得关于y的二次方程,将韦达定理代入上述表达式可得m的方程,解出即可.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形草坪AMPN中,点C在对角线MN上.CD垂直于AN于点D,CB垂直于AM于点B,|CD|=|AB|=3米,|AD|=|BC|=2米,设|DN|=x米,|BM|=y米.求这块矩形草坪AMPN面积的最小值. 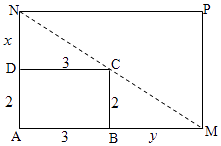
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数p:x2﹣4x﹣12≤0,q:(x﹣m)(x﹣m﹣1)≤0
(1)若m=2,那么p是q的什么条件;
(2)若q是p的充分不必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(a﹣ ![]() )(a∈R).若关于x的方程ln[(4﹣a)x+2a﹣5]﹣f(x)=0的解集中恰好有一个元素,则实数a的取值范围为 .
)(a∈R).若关于x的方程ln[(4﹣a)x+2a﹣5]﹣f(x)=0的解集中恰好有一个元素,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆(x+1)2+y2=8内有一点P(﹣1,2),AB过点P,
(1)若弦长 ![]() ,求直线AB的倾斜角;
,求直线AB的倾斜角;
(2)若圆上恰有三点到直线AB的距离等于 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,E为棱SC的中点,若AC=2 ![]() ,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( )
,SA=SB=AB=BC=SC=2,则异面直线AC与BE所成的角为( ) 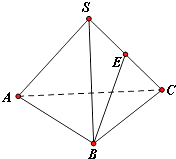
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() 的离心率
的离心率 ![]() ,椭圆上一点A到椭圆C两焦点的距离之和为4.
,椭圆上一点A到椭圆C两焦点的距离之和为4.
(1)求椭圆C的方程;
(2)直线l与椭圆交于A,B两点,且AB中点为 ![]() ,求直线l方程.
,求直线l方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)对任意的x都有f(x+2)﹣f(x)=﹣4x+4,且f(0)=0.
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+m,(m∈R). ①若存在实数a,b(a<b),使得g(x)在区间[a,b]上为单调函数,且g(x)取值范围也为[a,b],求m的取值范围;
②若函数g(x)的零点都是函数h(x)=f(f(x))+m的零点,求h(x)的所有零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x﹣2x .
)x﹣2x .
(1)若f(x)= ![]() ,求x的值;
,求x的值;
(2)若不等式f(2m﹣mcosθ)+f(﹣1﹣cosθ)<f(0)对所有θ∈[0, ![]() ]都成立,求实数m的取值范围.
]都成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com