
ЁОЬтФПЁПФГЫЎЯЩЛЈОгЊВПУПЬьЕФЗПзтЁЂЫЎЕчЁЂШЫЙЄЕШЙЬЖЈГЩБОЮЊ1000дЊЃЌУПХшЫЎЯЩЛЈЕФНјМлЪЧ10дЊЃЌЯњЪлЕЅМл![]() (дЊ) (
(дЊ) (![]() )гыШеОљЯњЪлСП
)гыШеОљЯњЪлСП![]() (Хш)ЕФЙиЯЕШчЯТБэЃЌВЂБЃжЄОгЊВПУПЬьгЏРћЃЎ
(Хш)ЕФЙиЯЕШчЯТБэЃЌВЂБЃжЄОгЊВПУПЬьгЏРћЃЎ
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
| 20 | 35 | 40 | 50 |
| 400 | 250 | 200 | 100 |
(Ђё) дкЫљИјЕФзјБъЭМжНжаЃЌИљОнБэжаЬсЙЉЕФЪ§ОнЃЌУшГіЪЕЪ§Жд![]() ЕФЖдгІЕуЃЌВЂШЗЖЈ
ЕФЖдгІЕуЃЌВЂШЗЖЈ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈЂђЃЉЧѓГі![]() ЕФжЕЃЌВЂНтЪЭЦфЪЕМЪвтвхЃЛ
ЕФжЕЃЌВЂНтЪЭЦфЪЕМЪвтвхЃЛ
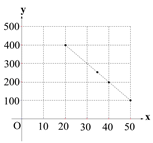
ЃЈЂѓЃЉЧыаДГіИУОгЊВПЕФШеЯњЪлРћШѓ![]() ЕФБэДяЪНЃЌВЂЛиД№ИУОгЊВПдѕбљЖЈМлВХФмЛёзюДѓШеЯњЪлРћШѓЃП
ЕФБэДяЪНЃЌВЂЛиД№ИУОгЊВПдѕбљЖЈМлВХФмЛёзюДѓШеЯњЪлРћШѓЃП
ЁОД№АИЁП(1)МћНтЮі;(2)МћНтЮі;(3)МћНтЮіЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈIЃЉУшЕуЛЭМЕУЕНвЛЬѕжБЯпЃЌЩшжБЯп![]() ЃЌДњШыСНЕуЧѓЕУжБЯпЗНГЬЃЛЃЈЂђЃЉИљОнЃЈIЃЉЕФНсЙћПЩжЊЃЌЕЅЮЛМлИёУПЩЯеЧ1дЊЃЌЯњЪлСПМѕЩй10ХшЃЛЃЈЂѓЃЉ
ЃЌДњШыСНЕуЧѓЕУжБЯпЗНГЬЃЛЃЈЂђЃЉИљОнЃЈIЃЉЕФНсЙћПЩжЊЃЌЕЅЮЛМлИёУПЩЯеЧ1дЊЃЌЯњЪлСПМѕЩй10ХшЃЛЃЈЂѓЃЉ![]() ЃЌИљОнЖЈвхгђЧѓЖўДЮКЏЪ§ЕФзюДѓжЕ.
ЃЌИљОнЖЈвхгђЧѓЖўДЮКЏЪ§ЕФзюДѓжЕ.
ЯъНтЃК(Ђё)гЩЬтБэзїГі![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЖдгІЕуЃЌЫќУЧЗжВМдквЛЬѕжБЯпЩЯЃЌШчЭМЫљЪОЃЎ
ЕФЖдгІЕуЃЌЫќУЧЗжВМдквЛЬѕжБЯпЩЯЃЌШчЭМЫљЪОЃЎ
 ЩшЫќУЧЙВЯпгк
ЩшЫќУЧЙВЯпгк![]() ЃЌдђШЁСНЕу
ЃЌдђШЁСНЕу![]() ЃЌ
ЃЌ![]() ЕФзјБъДњШыЕУ
ЕФзјБъДњШыЕУ
![]()
![]()
Ёр![]() (
(![]() ЃЌЧв
ЃЌЧв![]() )ЃЌ
)ЃЌ
ОМьбщ![]() ЃЌ
ЃЌ![]() вВдкДЫжБЯпЩЯЃЎ
вВдкДЫжБЯпЩЯЃЎ
ЁрЫљЧѓКЏЪ§НтЮіЪНЮЊ![]() (
(![]() ЃЌЧв
ЃЌЧв![]() )ЃЎ
)ЃЎ
ЃЈЂђЃЉгЩ(Ђё)ПЩЕУ![]() ЃЌЪЕМЪвтвхБэЪОЃКЯњЪлЕЅМлУПЩЯеЧ
ЃЌЪЕМЪвтвхБэЪОЃКЯњЪлЕЅМлУПЩЯеЧ![]() дЊЃЌШеЯњЪлСПМѕЩй
дЊЃЌШеЯњЪлСПМѕЩй![]() ХшЃЎ
ХшЃЎ
ЃЈЂѓЃЉвРЬтвт![]()
![]()
![]() (
(![]() ЃЌЧв
ЃЌЧв![]() ).
).
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЌЙЪЯњЪлЕЅМлЖЈЮЊ
ЃЌЙЪЯњЪлЕЅМлЖЈЮЊ![]() дЊЪБЃЌВХФмЛёЕУзюДѓШеЯњЪлРћШѓЃЎ
дЊЪБЃЌВХФмЛёЕУзюДѓШеЯњЪлРћШѓЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌНЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЫљЖдЕФБпЗжБ№ЮЊ
ЫљЖдЕФБпЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌcЃЎвбжЊ
ЃЌcЃЎвбжЊ![]() ЃЎ
ЃЎ
дђНЧ![]() ЕФДѓаЁ________
ЕФДѓаЁ________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП
вбжЊКЏЪ§![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌМЧКЏЪ§
ЃЌМЧКЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЖЈвхгђ
ЕФЖЈвхгђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() ЕФзюДѓжЕЮЊ
ЕФзюДѓжЕЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєЖдгк![]() ФкЕФШЮвтЪЕЪ§
ФкЕФШЮвтЪЕЪ§![]() ЃЌВЛЕШЪН
ЃЌВЛЕШЪН![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌвдзјБъдЕуЮЊМЋЕуЃЌ ![]() жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎвбжЊЕу
жсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎвбжЊЕу ![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ ![]() ЃЌжБЯп
ЃЌжБЯп ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ ![]() ЃЌЧвЕу
ЃЌЧвЕу ![]() дкжБЯп
дкжБЯп ![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ1ЃЉЧѓ ![]() ЕФжЕМАжБЯп
ЕФжЕМАжБЯп ![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉдВ ![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ ![]() ЃЌЪдХаЖЯжБЯп
ЃЌЪдХаЖЯжБЯп ![]() гыдВ
гыдВ ![]() ЕФЮЛжУЙиЯЕЃЎ
ЕФЮЛжУЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛИФЩЦОгУёЩњЛюЃЌЪаеаЩЬОжв§НјЭтЩЬЕНПЊЗЂЧјвЛДЮадЭЖзЪ72ЭђдЊНЈЦ№СЫвЛзљЪпВЫМгЙЄГЇ.вдКѓУПФъЛЙашвЊМЬајЭЖзЪЃКЕквЛФъашвЊвЊИїжжОЗбЮЊ12ЭђдЊЃЌДгЕкЖўФъПЊЪМУПФъЫљашОЗбОљБШЩЯвЛФъдіМг4ЭђдЊЃЌИУМгЙЄГЇУПФъЯњЪлзмЪеШыЮЊ50ЭђдЊ.
ЃЈ1ЃЉШєПлГ§ЭЖзЪМАИїжжОЗбЃЌИУМгЙЄГЇДгЕкМИФъПЊЪМДПРћШѓЮЊе§ЃП
ЃЈ2ЃЉШєИЩФъКѓЃЌЭтЩЬЮЊПЊЗЂаТЯюФПЃЌЖдМгЙЄГЇгаСНжжДІРэЗНАИЃК
ЂйШєФъЦНОљДПРћШѓДяЕНзюДѓжЕЪБЃЌБувд48ЭђдЊМлИёГіЪлИУГЇЃЛ
ЂкШєДПРћШѓзмКЭДяЕНзюДѓжЕЪБЃЌБувд16ЭђдЊЕФМлИёГіЪлИУГЇ.
ЮЪЃКФФвЛжжЗНАИБШНЯКЯЫуЃПЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшКЏЪ§fЃЈxЃЉ=|x+ ![]() |+|xЉa|ЃЈaЃО0ЃЉЃЎ
|+|xЉa|ЃЈaЃО0ЃЉЃЎ
ЃЈ1ЃЉжЄУїЃКfЃЈxЃЉЁн2ЃЛ
ЃЈ2ЃЉШєfЃЈ3ЃЉЃМ5ЃЌЧѓaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() ЕФЧАnЯюКЭЮЊ
ЕФЧАnЯюКЭЮЊ![]() ,ЧвТњзу
,ЧвТњзу![]() +n=2
+n=2![]() (nЁЪ
(nЁЪ![]() )
)
(1)жЄУї:Ъ§Са![]() ЮЊЕШБШЪ§Са,ВЂЧѓЪ§Са
ЮЊЕШБШЪ§Са,ВЂЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪН;
ЕФЭЈЯюЙЋЪН;
(2)Ъ§Са![]() Тњзу
Тњзу![]() (nЁЪ
(nЁЪ![]() ),ЦфЧАnЯюКЭЮЊ
),ЦфЧАnЯюКЭЮЊ![]() ,ЪдЧѓТњзу
,ЪдЧѓТњзу![]() +
+![]() >2018ЕФзюаЁе§ећЪ§n.
>2018ЕФзюаЁе§ећЪ§n.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§Ртжљ![]() ЕФЕзУцЪЧе§Ш§НЧаЮЃЌВрУц
ЕФЕзУцЪЧе§Ш§НЧаЮЃЌВрУц![]() ЮЊСтаЮЃЌЧв
ЮЊСтаЮЃЌЧв![]() ЃЌЦНУц
ЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЕФжаЕу.
ЕФжаЕу.
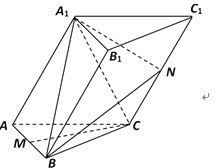
ЃЈIЃЉЧѓжЄЃК![]() ЁЮЦНУц
ЁЮЦНУц![]() ЃЛ
ЃЛ
ЃЈIIЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈIIIЃЉЧѓBA1гыЦНУц![]() ЫљГЩНЧЕФДѓаЁЃЎ
ЫљГЩНЧЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнвЊЧѓЧѓжЕЃК
ЃЈ1ЃЉгУеЗзЊЯрГ§ЗЈЧѓ123КЭ48ЕФзюДѓЙЋдМЪ§ЃЎ
ЃЈ2ЃЉгУИќЯрМѕЫ№ЪѕЧѓ80КЭ36ЕФзюДѓЙЋдМЪ§ЃЎ
ЃЈ3ЃЉАб89ЛЏЮЊЖўНјжЦЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com