
【题目】给出下列命题,其中正确命题的个数为( )
①若样本数据![]() ,
,![]() ,…,
,…,![]() 的方差为2,则数据
的方差为2,则数据![]() ,
,![]() ,…,
,…,![]() 的方差为4;
的方差为4;
②回归方程为![]() 时,变量x与y具有负的线性相关关系;
时,变量x与y具有负的线性相关关系;
③随机变量X服从正态分布![]() ,
,![]() ,则
,则![]() ;
;
④甲同学所在的某校高三共有5003人,先剔除3人,再按系统抽样的方法抽取容量为200的一个样本,则甲被抽到的概率为![]() .
.
A.1个B.2个C.3个D.4个
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中动圆P与圆![]() 外切,与圆
外切,与圆![]() 内切.
内切.
(1)求动圆圆心P的轨迹方程;
(2)直线l过点![]() 且与动圆圆心P的轨迹交于A、B两点.是否存在
且与动圆圆心P的轨迹交于A、B两点.是否存在![]() 面积的最大值,若存在,求出
面积的最大值,若存在,求出![]() 的面积的最大值;若不存在,说明理由.
的面积的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
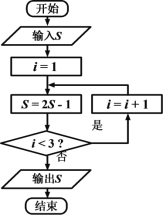
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为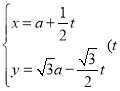 为参数,
为参数,![]() .在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线
.在以坐标原点为极点、x轴的非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,求直线
上,求直线![]() 的极坐标方程;
的极坐标方程;
(2)已知![]() ,若点
,若点![]() 在直线
在直线![]() 上,点
上,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着国内疫情形势好转,暂停的中国正在重启,为了尽快提升经济、吸引顾客,哈西某商场举办购物抽奖活动,凡当日购物满1000元的顾客,可参加抽奖,规则如下:盒中有大小质地均相同5个球,其中2个红球和3个白球,不放回地依次摸出2个球,若在第一次和第二次均摸到红球则获得特等奖,否则获得纪念奖,则顾客获得特等奖的概率是_________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共![]() 人,现从中抽取了
人,现从中抽取了![]() 人的数学成绩,绘制成频率分布直方图(如下图所示).已知这
人的数学成绩,绘制成频率分布直方图(如下图所示).已知这![]() 人中
人中![]() 分数段的人数比
分数段的人数比![]() 分数段的人数多
分数段的人数多![]() 人.
人.
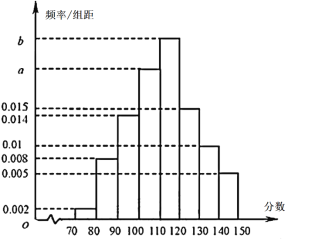
(1)根据频率分布直方图,求![]() 、
、![]() 的值,并估计抽取的
的值,并估计抽取的![]() 名同学数学成绩的中位数;
名同学数学成绩的中位数;
(2)若学年打算给数学成绩不低于![]() 分的同学颁发“网络课堂学习优秀奖”,将这
分的同学颁发“网络课堂学习优秀奖”,将这![]() 名同学数学成绩的样本频率视为概率.
名同学数学成绩的样本频率视为概率.
(i)估计全学年的获奖人数;
(ii)若从全学年随机选取![]() 人,求所选
人,求所选![]() 人中至少有
人中至少有![]() 人获奖的概率.
人获奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com