

分析 (1)首先根据题中的已知条件求出相关的线段长,然后根据所求的结果来进一步判断线面垂直,最后转化为线线垂直.
(2)取AD的中点F,则EF⊥平面ABCD,再求四棱锥E-ABCD的体积.
解答  (1)证明:梯形ABCE中,AB∥CE,D是CE中点,BC∥AD,AB=BC=2,∠BAD=60°连结BE交AD于M点,
(1)证明:梯形ABCE中,AB∥CE,D是CE中点,BC∥AD,AB=BC=2,∠BAD=60°连结BE交AD于M点,
在△ABE中利用余弦定理:BE2=AE2+AB2-2AE•ABcos∠EAB,
解得:BE=2$\sqrt{3}$且△ABE为等边三角形,EM=EB=$\sqrt{3}$,
AD⊥EM,
根据梯形的边角关系求得:AD⊥BM,
∴AD⊥面EMB,
∴BE?面EMB,
∴AD⊥BE;
(2)解:取AD的中点F,则EF⊥AD,
∵EF⊥AD,平面EAD⊥平面ABCD,平面EAD⊥平面ABCD=AD,
∴EF⊥平面ABCD,
∵EF=$\sqrt{3}$,SABCD=AB•ADsin60°=2×2×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴VE-ABCD=$\frac{1}{3}×2\sqrt{3}×\sqrt{3}$=2.
点评 本题考查的勾股定理及余弦定理,线面垂直的判定及性质定理,考查四棱锥E-ABCD的体积,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
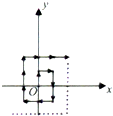 如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )
如图所示,质点A从坐标原点O开始沿箭头所指方向作规则运动,每次只运动一个单位,相应的质点的坐标记为An,如A1(0,1),A2(1,1),A3(1,0),A4(1,-1),…,则A2015的坐标为( )| A. | (-21,12) | B. | (-22,12) | C. | (-21,13) | D. | (-22,13) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{2}\sqrt{21}$ | B. | $\frac{25}{4}$ | C. | $\frac{15}{4}$ | D. | $\frac{3}{2}\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $-\frac{7}{25}$ | C. | $\frac{24}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 9 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arcsin1=$\frac{π}{2}$ | B. | arccos(-1)=π | C. | arctan0=0 | D. | arccos1=2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com