
����Ŀ������ѧ��ͨ���о�ѧ����ѧϰ��Ϊ���֣�ѧ���Ľ�����������ʦ�������������������õ�ʱ����أ���ѧ��ʼʱ��ѧ������Ȥ������ѧ������Ȥ����һ�ν������״̬�����ѧ����ע������ʼ��ɢ�����������ʵ���������f��x����ʾѧ�����պͽ��ܸ����������x��ʾ���ڸ����ʱ�䣨��λ��min�����������µĹ�ϵ��f��x��= 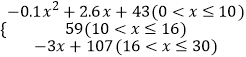
���������5min�뿪�����20min�Ƚϣ�ѧ���Ľ���������ʱ��ǿһЩ��
�����������minѧ���Ľ���������ǿ����ά�ֶ���ʱ�䣿
������һ������ѧ������Ҫ55���ϣ�����55���Ľ��������Լ�13minʱ�䣬��ô��ʦ�ܷ���ѧ��һֱ�ﵽ�������������״̬�½�����������
���𰸡��⣺��������f��x��= 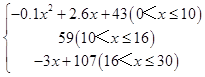 ��
��
����f��5��=53.5��f��20��=47����f��5����f��20��
�����5min�ȿ������20min��ѧ���Ľ���������ǿһЩ��
����0��x��10ʱ��f��x��=��0.1��x��13��2+59.9��
��x=10ʱ��f��x��min=f��10��=59��
��x��16ʱ��f��x������3��16+109=59��
�ʿ�����10min������10���ӣ�ѧ���Ľ���������ǿ����ά��6 min��
������ 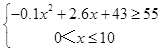 ��6��x��10��
��6��x��10��
�� ![]() ��16��x
��16��x ![]()
��t=��10��6��+6+�� ![]() ��6��=
��6��= ![]() ��13��
��13��
����ʦ������ѧ��һֱ�ﵽ�������������״̬�½������������
����������һС��Ƚ�5���Ӻ�20����ѧ���Ľ���������ʱǿ�������ǰ�x=5�����һ�κ����У���x=20Ҫ���뵽�ڶ��κ����У��Ƚϴ�С���ɣ���ͬ���Ա���������Ӧ�Ľ���ʽ���ܷ���Ҫ��
�ڶ�С����ѧ���Ľ���������ǿ��ʵ����Ҫ��ֶκ��������ֵ�������Ƿֱ�������ε����ֵȡ����ɣ�
����С�⿼��ֶκ���ͼ��������ԣ���f��x����55���ֱ���0��x��10ʱ��x��16ʱ��x�ķ�Χ����������ij��ȣ��������13min�Ƚϼ��ɵõ���


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��= ![]() �Ƕ����ڣ����ޣ�+�ޣ��ϵ��溯������f��
�Ƕ����ڣ����ޣ�+�ޣ��ϵ��溯������f�� ![]() ��=
��= ![]() ��
��
��1����ʵ��a��b����ȷ������f��x���Ľ���ʽ��
��2���ж�f��x���ڣ���1��1���ϵĵ����ԣ����ö���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ΪR�ĺ���f��x��= ![]() ��x��+bf��x��+c=0ǡ��5����ͬ��ʵ����x1 �� x2 �� x3 �� x4 �� x5 �� ��f��x1+x2+x2+x4+x5������ �� ��
��x��+bf��x��+c=0ǡ��5����ͬ��ʵ����x1 �� x2 �� x3 �� x4 �� x5 �� ��f��x1+x2+x2+x4+x5������ �� ��
A.0
B.21g2
C.31g2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0��a��1������f��x��=a ![]() �����ֵ����ʽloga��x2��5x+7����0�Ľ⼯Ϊ ��
�����ֵ����ʽloga��x2��5x+7����0�Ľ⼯Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±��ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���x(��)����Ӧ�������ܺ�y(�ֱ�ú)�ļ����������.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)�뻭���ϱ����ݵ�ɢ��ͼ��
(2)������ϱ��ṩ�����ݣ�����С���˷����y����x�����Իع鷽��![]() ��
��
(3)��֪�ó�����ǰ100�ּײ�Ʒ�������ܺ�Ϊ90�ֱ�ú���Ը���(2)��������Իع鷽�̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ���ǰ���Ͷ��ٶֱ�ú��
�ο���ʽ�� 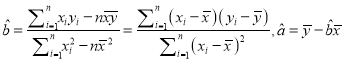 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2+bx+1����f��1+x��=f��1��x���� ![]() ��
��
��1������f��x���Ľ���ʽ��
��2���ж�g��x����[1��2]�ϵĵ����Բ��ö���֤����Ľ��ۣ�
��3����g��x����[1��2]�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() ��
��
��1������f��x���Ķ�����
��2���жϺ���f��x������ż�ԣ�
��3����֤��f��x����0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������X��Y�����������£�
y1 | y2 | �ܼ� | |
x1 | a | b | a+b |
x2 | c | d | c+d |
�ܼ� | a+c | b+d | a+b+c+d |
������˵������ȷ���ǣ� ��
A.ad��bcԽС��˵��X��Y��ϵԽ��
B.ad��bcԽ��˵��X��Y��ϵԽǿ
C.(ad��bc)2Խ��˵��X��Y��ϵԽǿ
D.(ad��bc)2Խ�ӽ���0��˵��X��Y��ϵԽǿ
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com