
【题目】设有限数列![]() ,定义集合
,定义集合![]() 为数列
为数列![]() 的伴随集合.
的伴随集合.
(Ⅰ)已知有限数列![]() 和数列
和数列![]() .分别写出
.分别写出![]() 和
和![]() 的伴随集合;
的伴随集合;
(Ⅱ)已知有限等比数列![]() ,求
,求![]() 的伴随集合
的伴随集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差数列![]() ,判断
,判断![]() 是否能同时属于
是否能同时属于![]() 的伴随集合
的伴随集合![]() ,并说明理由.
,并说明理由.
【答案】(Ⅰ)数列![]() 的伴随集合为
的伴随集合为![]() ,数列
,数列![]() 的伴随集合为
的伴随集合为![]() ;(Ⅱ)
;(Ⅱ)![]() (Ⅲ)不能
(Ⅲ)不能
【解析】
(Ⅰ)由数列A的伴随集合定义可得P,Q的伴随集合;
(Ⅱ)先证明对任意i≠k或j≠l,则ai+aj≠ak+al(1≤i<j≤n,1≤k<l≤n),可得求集合M中各元素之和时,每个ai(1≤i≤n)均出现n﹣1次,由等比数列的求和公式,计算可得所求和;
(Ⅲ)假设![]() 同时属于数列A的伴随集合M.设数列A的公差为d(d≠0),运用等差数列的定义和通项公式、性质,推理论证得到矛盾,即可判断.
同时属于数列A的伴随集合M.设数列A的公差为d(d≠0),运用等差数列的定义和通项公式、性质,推理论证得到矛盾,即可判断.
解:(Ⅰ)数列![]() 的伴随集合为
的伴随集合为![]() ,数列
,数列![]() 的伴随集合为
的伴随集合为![]() .
.
(Ⅱ)先证明对任意![]() 或
或![]() ,则
,则![]() .
.
假设![]() .
.
当![]() 且
且![]() ,因为
,因为![]() ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,与
,与![]() 矛盾.
矛盾.
同理,当![]() 且
且![]() 时,也不成立.
时,也不成立.
当![]() 且
且![]() 时,不妨设
时,不妨设![]() ,因为
,因为![]() ,则
,则![]() ,
,
所以![]() ,
,
左边为奇数,右边为偶数,所以![]() ,
,
综上,对任意![]() 或
或![]() ,则
,则![]()
所以求集合![]() 中各元素之和时,每个
中各元素之和时,每个![]() 均出现
均出现![]() 次,
次,
所以![]()
![]()
(Ⅲ)假设![]() 同时属于数列
同时属于数列![]() 的伴随集合
的伴随集合![]() .
.
设数列![]() 的公差为
的公差为![]() ,则
,则
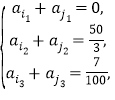 即
即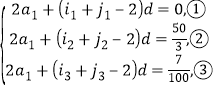
②-①得,![]() ,
,
③-①得,![]() ,
,
两式相除得,![]() ,
,
因为![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() .
.
又因为![]() ,
,
所以![]() ,
,
![]() ,
,
所以![]() ,与
,与![]() 矛盾,
矛盾,
所以![]() 不能同时属于数列
不能同时属于数列![]() 的伴随集合
的伴随集合![]() .
.


科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]()
![]() ,过抛线
,过抛线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于A、B两点,分别交抛物线于E、F两点,圆心点
相切于A、B两点,分别交抛物线于E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
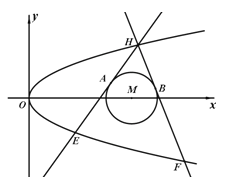
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)当![]() 的角平分线垂直x轴时,求直线EF的斜率;
的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,左顶点为
,左顶点为![]() ,过椭圆
,过椭圆![]() 的右焦点
的右焦点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 和
和![]() ,分别交直线
,分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最小值;
的面积的最小值;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,椭圆
,椭圆![]() 的右顶点为
的右顶点为![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在首届中国国际商品博览会期间,甲、乙、丙三家供货公司各签订了两个供货合同,已知这三家公司供货合同中金额分别是300万元和600万元、300万元和900万元、600万元和900万元,甲看了乙的供货合同说:“我与乙的供货合同中金额相同的合同不是600万元”,乙看了丙的供货合同说:“我与丙的供货合同中金额相同的合同不是300万元”,丙说:“我的两个供货合同中金额之和不是1500万元”,则甲签订的两个供货合同中金额之和是( )
A.900万B.1500万元C.不能确定D.1200万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其右焦点为
,其右焦点为![]() ,以坐标原点
,以坐标原点![]() 为圆心,椭圆短半轴长为半径的圆与直线
为圆心,椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆![]() 的方程;
的方程;
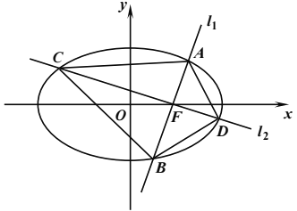
(Ⅱ)经过点![]() 的直线
的直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 及
及![]() ,
,![]() 四点,且
四点,且![]() ,探究:是否存在常数
,探究:是否存在常数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是正整数.在一个十进制
是正整数.在一个十进制![]() 位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的
位数的各位数字中,若含有数字8,则在每个数字8的前一位数字就不能是数字3(即不能出现38字样).试求出所有这样的![]() 位数的个数.
位数的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“吸烟有害健康,吸烟会对身体造成伤害”,哈尔滨市于2012年5月31日规定室内场所禁止吸烟.美国癌症协会研究表明,开始吸烟年龄X分别为16岁、18岁、20岁和22岁者,其得肺癌的相对危险度Y依次为15.10,12.81,9.72,3.21;每天吸烟支数U分别为10,20,30者,其得肺癌的相对危险度V分别为7.5,9.5和16.6,用![]() 表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
表示变量X与Y之间的线性相关系数,用r2表示变量U与V之间的线性相关系数,则下列说法正确的是( )
A.r1=r2B.r1>r2>0
C.0<r1<r2D.r1<0<r2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com