
已知函数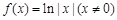 ,函数
,函数 .
.
(1)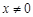 时,求函数
时,求函数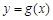 的表达式;
的表达式;
(2)若a > 0,函数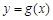 在
在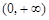 上的最小值是2,求a的值;
上的最小值是2,求a的值;
(3)在 (2) 的条件下,求直线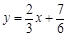 与函数
与函数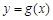 的图象所围成图形的面积.
的图象所围成图形的面积.
(1)当 时,
时,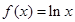 ; 当
; 当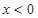 时,
时,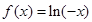
∴当 时,
时,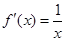 ; 当
; 当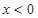 时,
时,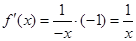 .
.
∴当 时,函数
时,函数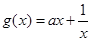 4分
4分
(2) 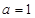 .(3)
.(3)
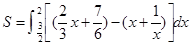 =
=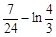 。
。
【解析】本试题主要是考查了导数的运算,以及运用导数求解函数的最值,和定积分的几何意义求解曲边梯形的面积的综合运用
(1)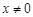 时,利用f(x)和f’(x)得到函数
时,利用f(x)和f’(x)得到函数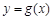 的表达式;
的表达式;
(2)因为a > 0,对于函数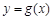 在
在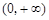 上的最小值是2,分析单调性确定最值在那个点取得为关键,
上的最小值是2,分析单调性确定最值在那个点取得为关键,
(3)在 (2) 的条件下,求直线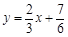 与函数
与函数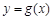 的图象所围成图形的面积,利用定积分的几何意义得到。
的图象所围成图形的面积,利用定积分的几何意义得到。
解:(1) ∵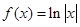 ,
,
∴当 时,
时,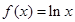 ; 当
; 当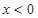 时,
时,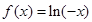
∴当 时,
时,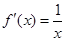 ; 当
; 当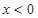 时,
时,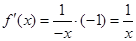 .
.
∴当 时,函数
时,函数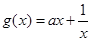 4分
4分
(2) ∵由⑴知当 时,
时,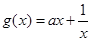 ,
,
∴当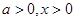 时,
时,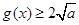 当且仅当
当且仅当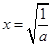 时取等号.
时取等号.
∴函数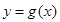 在
在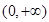 上的最小值是
上的最小值是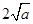 ,由已知
,由已知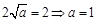
∴依题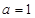 .
.
(3) 由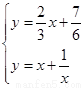 解得
解得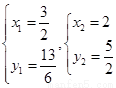
∴直线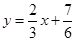 与函数
与函数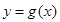 的图象所围成图形的面积
的图象所围成图形的面积
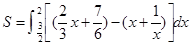 =
=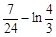 12分
12分


科目:高中数学 来源: 题型:
| a |
| x |
| 1 |
| x |
| 4 |
| x |
| b2 |
| x |
| 8 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示: 已知函数f(x)的定义域为[-2,+∞),部分对应值如表格所示,f′(x)为f(x).的导函数,函数y=f′(x)的图象如右图所示:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com