
【题目】2020年4月8日零时正式解除离汉通道管控,这标志着封城76天的武汉打开城门了.在疫情防控常态下,武汉市有序复工复产复市,但是仍然不能麻痹大意仍然要保持警惕,严密防范、慎终如始.为科学合理地做好小区管理工作,结合复工复产复市的实际需要,某小区物业提供了A,B两种小区管理方案,为了决定选取哪种方案为小区的最终管理方案,随机选取了4名物业人员进行投票,物业人员投票的规则如下:①单独投给A方案,则A方案得1分,B方案得﹣1分;②单独投给B方案,则B方案得1分,A方案得﹣1分;③弃权或同时投票给A,B方案,则两种方案均得0分.前1名物业人员的投票结束,再安排下1名物业人员投票,当其中一种方案比另一种方案多4分或4名物业人员均已投票时,就停止投票,最后选取得分多的方案为小区的最终管理方案.假设A,B两种方案获得每1名物业人员投票的概率分别为![]() 和
和![]() .
.
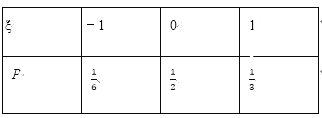
(1)在第1名物业人员投票结束后,A方案的得分记为ξ,求ξ的分布列;
(2)求最终选取A方案为小区管理方案的概率.
【答案】(1)分布列见解析;(2)![]() .
.
【解析】
(1) 由题意知,ξ的所有可能取值为﹣1,0,1,然后,列出ξ的分布列即可
(2) 记M1表示事件“前2名物业人员进行了投票,且最终选取A方案为小区管理方案”,
记M2表示事件“前3名物业人员进行了投票,且最终选取A方案为小区管理方案”,
记M3表示事件“共有4名物业人员进行了投票,且最终选取A方案为小区管理方案”,
记选取A方案为小区管理方案的概率为P,
然后分别求出![]() ,
,![]() ,
,![]() 的值,则选取A方案为小区管理方案的概率为:
的值,则选取A方案为小区管理方案的概率为:
![]() ,然后计算求解即可.
,然后计算求解即可.
(1)由题意知,ξ的所有可能取值为﹣1,0,1,
P(ξ=﹣1)=(1![]() )
)![]() ,P(ξ=0)
,P(ξ=0)![]() ,P(ξ=1)
,P(ξ=1)![]() ,
,
∴ξ的分布列为
(2)记M1表示事件“前2名物业人员进行了投票,且最终选取A方案为小区管理方案”,
由(1)知,![]() ,
,
记M2表示事件“前3名物业人员进行了投票,且最终选取A方案为小区管理方案”,
![]() ,
,
记M3表示事件“共有4名物业人员进行了投票,且最终选取A方案为小区管理方案”,
①若A方案比B方案多4分,有两类:
第一类,A方案前三次得了一次1分两次0分,最后一次得1分,其概率为![]() ;
;
第二类,A方案前两次得了一次1分一次﹣1分,后两次均得1分,其概率为![]() ,
,
②若A方案比B方案多2分,有三类:
第一类,A方案四次中得了一次1分,其他三次全0分,其概率为![]() ;
;
第二类,A方案前三次得了一次1分,一次0分,一次﹣1分,最后一次得了1分,其概率为![]() ;
;
第三类,A方案前两次得了一次1分一次﹣1分,第三次得1分,第四次得0分,其概率为![]() .
.
故![]() ,
,
∴最终选取A方案为小区管理方案的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】现有9位身高各异的同学拍照留念,分成前后两排,前排4人,后排5人,要求每排同学的身高从中间到两边依次递减,则不同的排队方式有________种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天干地支纪年法源于中国,中国自古便有十天干与十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥天干地支纪年法是按顺序以一个天干和一个地支相配,排列起来,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年为“甲子”,第二年为“乙丑”,第三年为“丙寅”,…,以此类推,排列到“癸酉”后,天于回到“甲”重新开始,即“甲戌”,“乙亥”,然后地支回到“子”重新开始,即“丙子”,以此类推已知1949年为“己丑”年,那么到中华人民共和国成立70年时为( )
A.丙酉年B.戊申年C.己申年D.己亥年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,△PAD为等边三角形,AB=AD![]() CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E为BC的中点.
CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E为BC的中点.
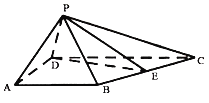
(1)证明:AD⊥PE.
(2)求直线PA与平面PDE所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,沿矩形对角线BD将
,沿矩形对角线BD将![]() 折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当
折起形成四面体ABCD,在这个过程中,现在下面四个结论:①在四面体ABCD中,当![]() 时,
时,![]() ;②四面体ABCD的体积的最大值为
;②四面体ABCD的体积的最大值为![]() ;③在四面体ABCD中,BC与平面ABD所成角可能为
;③在四面体ABCD中,BC与平面ABD所成角可能为![]() ;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
;④四面体ABCD的外接球的体积为定值.其中所有正确结论的编号为( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
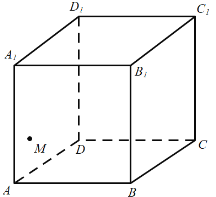
【题目】如图,点![]() 是正方体
是正方体![]() 中的侧面
中的侧面![]() 上的一个动点,则下列结论正确的是( )
上的一个动点,则下列结论正确的是( )
A.点![]() 存在无数个位置满足
存在无数个位置满足![]()
B.若正方体的棱长为1,三棱锥![]() 的体积最大值为
的体积最大值为![]()
C.在线段![]() 上存在点
上存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成的角是
所成的角是![]()
D.点![]() 存在无数个位置满足到直线
存在无数个位置满足到直线![]() 和直线
和直线![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
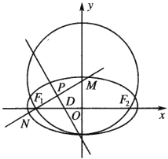
【题目】圆![]() 过椭圆
过椭圆![]() 的下顶点及左、右焦点
的下顶点及左、右焦点![]() ,
,![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() 的直线与椭圆
的直线与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() 且垂足为点
且垂足为点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:当直线![]() 斜率变化时
斜率变化时![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点与抛物线
右焦点与抛物线![]() 的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线
的焦点重合,以原点为圆心、椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆的方程
(2)若直线![]() 与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,
与y轴交点为P,A、B是椭圆上两个动点,它们在y轴两侧,![]() ,
,![]() 的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
的平分线与y轴重合,则直线AB是否过定点,若过定点,求这个定点坐标,若不过定点说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com