练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．某校为了调查高三年级学生某次联考数学成绩情况，用简单随机抽样，抽取了50名高三年级学生，以他们的数学成绩（百分制）作为样本，得到如下的频数分布表：
    频数[50，60）[60，70）[70，80）[80，90）[90，100]
    频数31319114
    （Ⅰ）若该校高三年级每位学生被抽取的概率为0.1，求该校高三年级学生的总人数；
    （Ⅱ）估计这次联考该校高三年级学生数学成绩的平均分及方差（同一组中的数据用该组区间的中点值作代表）；
    （Ⅲ）根据以上抽样数据，能否认为该校高三年级本次联考数学成绩符合“优秀（80分及80分以上为优秀）率不低于25%”的要求？

    分析 （Ⅰ）设高三年级的总人数为n，由$\frac{50}{n}$=0.1，解得即可；
    （Ⅱ），先求出各组成绩的频率，再根据平均数的公式和方差公式计算即可；
    （Ⅲ）成绩分数为优秀所占的比例的估计值为0.22+0.08=0.30，即可的判断符合要求．

    解答 解：（Ⅰ）设高三年级的总人数为n，由$\frac{50}{n}$=0.1，得到n=500，
    所以高三年级的总人数为500人，
    （Ⅱ）以题意，求得各组成绩的频率分别为0.06，0.26，0.38，0.22，0.08，
    所以成绩的平均分为$\overline{x}$=55×0.06+65×0.26+75×0.38+85×0.22+95×0.08=75，
    成绩的样本方差为s2=（-20）2×0.06+（-10）2×0.26+0×0.38+102×0.22+202×0.08=104，
    所以估计这次联考该校高三年级学生数学成绩的平均分为75分，方差为1-4，
    （Ⅲ）成绩分数为优秀所占的比例的估计值为0.22+0.08=0.30，
    由于该估计值大于25%，所以该校高三年级本次联考数学成绩符合“优秀（80分及80分以上为优秀）率不低于25%”的要求．

    点评 本题考查了频率统计表的应用问题，解题时应根据图中数据进行有关的计算，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．已知（ax+1）n的展开式中有连续三项的二项式系数之比为1：2：3．
    （1）求n的值；
    （2）若展开式中含x的项的系数为112，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．先将函数y=sin2x的图象向右平移$\frac{π}{5}$个长度单位，然后将所得图象横坐标缩短到原来的$\frac{1}{2}$，纵坐标不变，此时函数的解析式为（　　）
    A．y=sin（4x-$\frac{2π}{5}$）B．y=sin（4x-$\frac{π}{5}$）C．y=sin（x-$\frac{2π}{5}$）D．y=sin（x-$\frac{π}{5}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．设复数z1=a+2i，z2=4-3i，
    （1）当a=1时，求复数z1z2的模；
    （2）已知$\frac{{z}_{1}}{{z}_{2}}$为纯虚数，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知向量$\overrightarrow{a}$、$\overrightarrow{b}$是平面内两个互相垂直的单位向量，且（3$\overrightarrow{a}$-$\overrightarrow{c}$）$•（4\overrightarrow{b}-\overrightarrow{c}）$=0，则|$\overrightarrow{c}$|的最大值是（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．某几何体的三视图如图，则该几何体的体积为（　　）
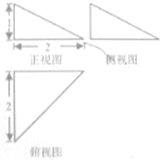
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设数列{an}满足a1=1，an+1=3an+2，则{an}的通项公式为（　　）
    A．an=2•3n-1B．an=2•3n-1-1C．an=2•3n-1+1D．an=2•3n+1-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知z=$\frac{i}{1+i}$，则在复平面内，复数z所对应的点在（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知圆锥SO的高为4，体积为4π，则底面半径r=$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案