
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函数f(x)在[t,t+2](t>0)上的最小值;
(2)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.
(3)探讨函数F(x)=lnx﹣ ![]() +
+ ![]() 是否存在零点?若存在,求出函数F(x)的零点,若不存在,请说明理由.
是否存在零点?若存在,求出函数F(x)的零点,若不存在,请说明理由.
【答案】
(1)解:f(x)=xlnx,
f′(x)=lnx+1,令f′(x)=0,解得x= ![]() .
.
① 当0<t< ![]() 时,在x∈[t,
时,在x∈[t, ![]() )上f′(x)<0;在x∈(
)上f′(x)<0;在x∈( ![]() .t+2]上f′(x)>0.
.t+2]上f′(x)>0.
因此,f(x)在x= ![]() 处取得极小值,也是最小值.fmin(x)=﹣
处取得极小值,也是最小值.fmin(x)=﹣ ![]() .
.
②当t≥ ![]() ,f′(x)≥0,因此f(x)在[t,t+2]上单调递增,
,f′(x)≥0,因此f(x)在[t,t+2]上单调递增,
∴fmin(x)=f(t)=tlnt
(2)解:由对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
即有2xlnx≥﹣x2+ax﹣3.
即a≤2lnx+x+ ![]() 恒成立,
恒成立,
令h(x)=2lnx+x+ ![]() ,h′(x)=
,h′(x)= ![]() +1﹣
+1﹣ ![]() =
= ![]() =
= ![]() ,
,
当x>1时,h′(x)>0,h(x)是增函数,
当0<x<1时,h′(x)<0,h(x)是减函数,
∴a≤h(x)min=h(1)=4.
即实数a的取值范围是(﹣∞,4]
(3)解:令m(x)=2xlnx,
m'(x)=2(1+lnx),
当x∈(0, ![]() )时,m'(x)<0,m(x)递减;
)时,m'(x)<0,m(x)递减;
当x∈( ![]() ,+∞)时,m'(x)>0,m(x)递增;
,+∞)时,m'(x)>0,m(x)递增;
∴m(x)的最小值为m( ![]() )=﹣
)=﹣ ![]() ,
,
则2xlnx≥﹣ ![]() ,
,
∴lnx≥﹣ ![]() ,
,
F(x)=lnx﹣ ![]() +
+ ![]() =0①
=0①
则F(x)=lnx﹣ ![]() +
+ ![]() ≥﹣
≥﹣ ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
令G(x)= ![]() ﹣
﹣ ![]() ,则G'(x)=
,则G'(x)= ![]() ,
,
当x∈(0,1)时,G'(x)<0,G(x)递减;
当x∈(1,+∞)时,G'(x)>0,G(x)递增;
∴G(x)≥G(1)=0 ②
∴F(x)=lnx﹣ ![]() +
+ ![]() ≥﹣
≥﹣ ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() )≥0,
)≥0,
∵①②中取等号的条件不同,
∴F(x)>0,故函数F(x)没有零点
【解析】(1)求得f′(x)=lnx+1,令f′(x)=0,可得x= ![]() .对t分类讨论:当0<m<
.对t分类讨论:当0<m< ![]() 时,及当t≥
时,及当t≥ ![]() 时,分别研究其单调性、极值与最值,即可得出;(2)由题意可得,2xlnx≥﹣x2+ax﹣3.即a≤2lnx+x+
时,分别研究其单调性、极值与最值,即可得出;(2)由题意可得,2xlnx≥﹣x2+ax﹣3.即a≤2lnx+x+ ![]() 恒成立,令h(x)=2lnx+x+
恒成立,令h(x)=2lnx+x+ ![]() ,求出导数和单调区间,可得极小值且为最小值,由此求出实数a的取值范围;(3)把函数整理成F(x)=lnx﹣
,求出导数和单调区间,可得极小值且为最小值,由此求出实数a的取值范围;(3)把函数整理成F(x)=lnx﹣ ![]() +
+ ![]() ≥﹣
≥﹣ ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),要判断是否有零点,只需看F(x)的正负问题,令G(x)=
),要判断是否有零点,只需看F(x)的正负问题,令G(x)= ![]() ﹣
﹣ ![]() ,利用导数分析G(x)的单调区间和最值,即可判断是否存在零点.
,利用导数分析G(x)的单调区间和最值,即可判断是否存在零点.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
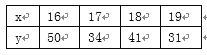
【题目】某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如下表所示:由表可得线性回归方程![]() 中的
中的![]() ,据此模型预测零售价为15元时,每天的销售量为_____个.
,据此模型预测零售价为15元时,每天的销售量为_____个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,设f(n)=an , 且f(n)满足f(n+1)﹣2f(n)=2n(n∈N*),且a1=1.
(1)设 ![]() ,证明数列{bn}为等差数列;
,证明数列{bn}为等差数列;
(2)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】银川一中从高二年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组:![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.

(1)求图中实数![]() 的值;
的值;
(2)试估计我校高二年级在这次数学考试的平均分;
(3)若从样本中数学成绩在![]() 与
与![]() 两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,求这两名学生的数学成绩之差的绝对值不大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的方程为
处的切线的方程为![]() ,求实数
,求实数![]() 的值;
的值;
(2)设![]() ,若对任意两个不等的正数
,若对任意两个不等的正数![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若在![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设m,n为不重合的两条直线,![]() ,
,![]() 为不重合的两个平面,则下列命题中,所有真命题的个数是______.
为不重合的两个平面,则下列命题中,所有真命题的个数是______.
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;
![]() 若
若![]() ,
,![]() ,则
,则![]() ;
;![]() 一定存在直线l,使得
一定存在直线l,使得![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 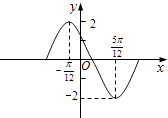
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,其长轴长与短轴长的和等于6.
,其长轴长与短轴长的和等于6.
(1)求椭圆E的方程;
(2)如图,设椭圆E的上、下顶点分别为A1、A2 , P是椭圆上异于A1、A2的任意一点,直线PA1、PA2分别交x轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.证明:线段OT的长为定值. 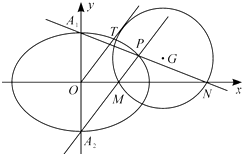
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com