
【题目】设x,y满足约束条件: 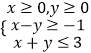 ;则z=x﹣2y的取值范围为 .
;则z=x﹣2y的取值范围为 .
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图所示,某人在M汽车站的北偏西20°的方向上的A处,观察到点C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°,开始时,汽车到A的距离为31千米,汽车前进20千米后,到A的距离缩短了10千米.问汽车还需行驶多远,才能到达M汽车站? 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理健康教育老师对某班50个学生进行了心里健康测评,测评成绩满分为100分.成绩出来后,老师对每个成绩段的人数进行了统计,并得到如图4所示的频率分布直方图. 
(1)求a,并从频率分布直方图中求出成绩的众数和中位数;
(2)若老师从60分以下的人中选两个出来与之聊天,则这两人一个在(40,50]这一段,另一个在(50,60]这一段的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)过点(
=1(a>b>0)过点( ![]() ,﹣
,﹣ ![]() ),且离心率为
),且离心率为 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点A(x1 , y1),B(x2 , y2)是椭圆C上的亮点,且x1≠x2 , 点P(1,0),证明:△PAB不可能为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述: ①函数 ![]() 是奇函数;
是奇函数;
②函数 ![]() 的一条对称轴方程为
的一条对称轴方程为 ![]() ;
;
③函数 ![]() ,
, ![]() ,则f(x)的值域为
,则f(x)的值域为 ![]() ;
;
④函数 ![]() 有最小值,无最大值.
有最小值,无最大值.
所有正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=6cos2 ![]() +
+ ![]() sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sinωx﹣3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形. 
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)= ![]() ,且x0∈(﹣
,且x0∈(﹣ ![]() ,
, ![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三女生身高情况,某中学对初三女生身高情况进行了一次测量,所得数据整理后列出了频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合计 | M | N |
(1)求出表中m,n,M,N所表示的数分别是多少?
(2)画出频率分布直方图;
(3)全体女生中身高在哪组范围内的人数最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com